Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'
Vẽ các tia Oz và O'z' lần lượt là tia phân giác của góc xOy và x'O'y' . Chứng tỏ:
a) Hai góc xOy và x'O'y' bằng nhau.
b) Oz // O'z'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 4 2018
- Từ O’ vẽ O’x’ // Ox
- Từ O’ vẽ O’y’//Oy sao cho góc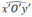 
là góc nhọn.
Ta được trường hợp hình vẽ trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 11 2023
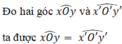
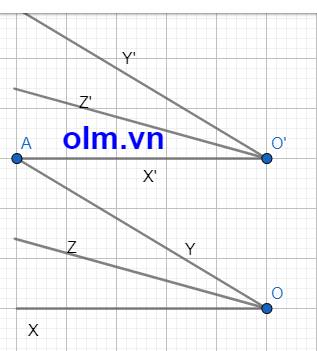
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 11 2023
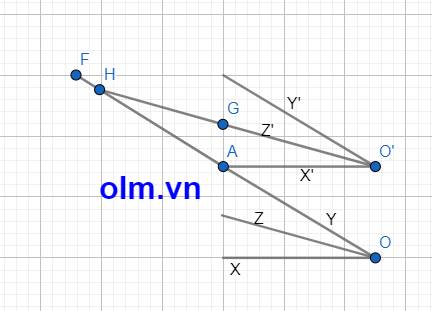
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)
1 tháng 9 2016
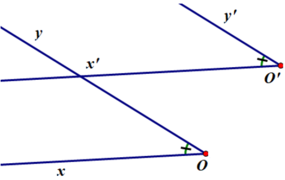
Cách vẽ:
- Từ O' vẽ O'x' //Ox.
- Từ O' Vẽ O'y' //Oy sao cho góc \(\widehat{x'O'y'}\) là góc nhọn. Ta được hai trường hợp hình vẽ sau:
Đo hai góc \(\widehat{xOy}\) và \(\widehat{x'O'y'}\) ta được \(\widehat{xOy}=\widehat{x'O'y'}\)
LT
0