\(=6+6+6+...+6\)

Tổng có \(\left[\left(95-5\right):6+1\right]:2=8\left(\text{số hạng }6\right)\)

Vậy tổng là \(8\cdot6=48\)

Anh ơi giúp em với 

lỗi r

? lỗi 

a: Để Δ//d1 thì \(\left\{{}\begin{matrix}m^2-2=2\\m-1\ne-3\end{matrix}\right.\Leftrightarrow m=2\)

b c d đi ạ

thi à

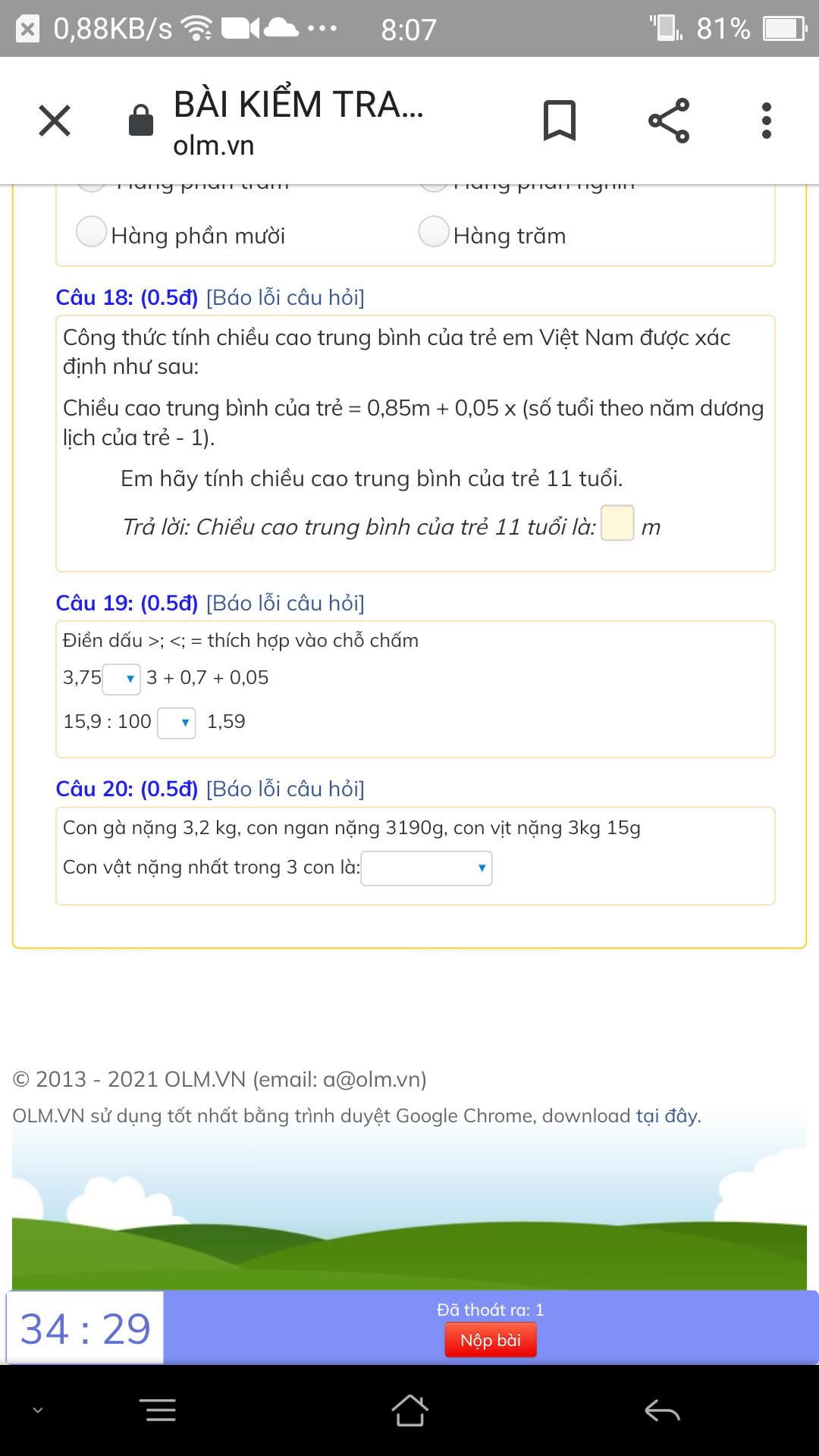
Câu 20:

Con gà nặng nhất

Câu 19: 

3,75=3+0,7+0,05

15,9:100<1,59

Thu được F1 có kiểu hình: 25% đỏ,kép:25% đỏ,đơn:25%trắng, kép:25% 25%trắng,đơn~1:1:1:1

=> có 4 tổ hợp giao tử. 4=2.2 hoặc 4=4.1

TH1:(2.2)

Kiểu gen: Aabb x aaBb 

P:    Aabb( đỏ,đơn) x    aaBb( trắng,kép)

Gp.    Ab,ab.                aB,ab

F1: 1AaBb:1Aabb:1aaBb:1aabb

kiêu gen:1A_B_:1A_bb:1aaB_:1aabb

kiểu hình:1 đỏ,kép:1đỏ,đơn:1trắng,kép:1trắng,đơn

TH2: (4.1)

Kiểu gen: AaBb x aabb

P:     AaBb( đỏ,kép).    x.  aabb( trắng,đơn)

Gp.  AB,Ab,aB,ab.          ab

F1: 1AaBb:1Aabb:1aaBb:1aabb

kiểu gen:1A_B_:1A_bb:1aaB_:1aabb

kiểu hình:1 đỏ,kép:1đỏ,đơn:1trắng,kép:1trắng,đơn

A đúng rồi bạn

a: BC=5cm

b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔABD=ΔHBD

c: \(\widehat{CHI}+\widehat{C}=90^0\)

\(\widehat{ABC}+\widehat{C}=90^0\)

Do đó: \(\widehat{CHI}=\widehat{ABC}\)

a: Ta có: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

=>\(BH=CH=\dfrac{6}{2}=3\left(cm\right)\)

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(HA^2=5^2-3^2=16\)

=>\(HA=\sqrt{16}=4\left(cm\right)\)

b: Xét ΔAHB có HE là phân giác

nên \(\dfrac{AE}{EB}=\dfrac{AH}{HB}=\dfrac{4}{3}\)(1)

=>\(\dfrac{AE}{4}=\dfrac{EB}{3}\)

mà AE+EB=AB=5cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AE}{4}=\dfrac{EB}{3}=\dfrac{AE+EB}{4+3}=\dfrac{5}{7}\)

=>\(AE=\dfrac{5}{7}\cdot4=\dfrac{20}{7}\left(cm\right)\)

c: Xét ΔAHC có HF là phân giác

nên \(\dfrac{AF}{FC}=\dfrac{AH}{HC}=\dfrac{4}{3}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AF}{FC}\)

Xét ΔABC có \(\dfrac{AE}{EB}=\dfrac{AF}{FC}\)

nên EF//BC

Ta có: EF//BC

BC\(\perp\)AH

Do đó: EF\(\perp\)AH

d: Xét ΔAHB vuông tại H có HE là đường cao

nên \(HE\cdot AB=HA\cdot HB\)

=>\(HE\cdot5=3\cdot4=12\)

=>\(HE=\dfrac{12}{5}=2,4\left(cm\right)\)

Xét ΔABC có EF//BC

nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)

=>\(\dfrac{EF}{6}=\dfrac{20}{7}:5=\dfrac{4}{7}\)

=>\(EF=\dfrac{24}{7}\left(cm\right)\)