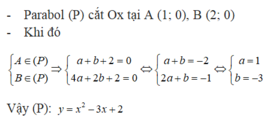1.Tìm pt parabol y=ax2+bx +3(a≠0)khi biết:
a. Hàm số y=f(x) đạt cực đại bằng 12 tại x=3
b. Parabol tiếp xúc với trục hoành tại x=-1
c. Parabol cắt trục hoành tại hai điểm M(-1;0)và N(-3;0)
d. Parabol qua điểm E(-1;9)và có trục đối xứng là x=-2
2. Xác định hàm số bậc 2 y=ax2+ bx+c(a≠0)biết rằng:
a. Hàm số triệt tiêu khi x=8 và đạt cực tiểu bằng -12 khi x=6
b. Hàm số có giá trị bằng -3 khi x= -1 và đạt cực đại bằng 13/4 khi x=3/2
3. Tìm pt của parabol y= ax2+bx+c(a≠0) biết:
a. Parabol qua 2 điểm A(2;-5);B(-1;16) và có trục đối xứng x=4
b. Parabol cắt trục hoành tại C(1;0) cắt trục tung tại D(0;5) và có trục đối xứng x=3