c) Để hàm số cắt trục tung tại điểm có tung độ âm thì:

m - 5 < 0

m < 0+ 5

m < 5 (nhận)

Vậy m < 5 và m ≠ 1 thì đồ thị của hàm số cắt trục tung tại điểm có tung độ âm

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:

\(AF\cdot AC=AK^2\left(1\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:

\(KB\cdot KC=AK^2\left(2\right)\)

Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)

b: Xét tứ giác AFKE có 

\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)

Do đó: AFKE là hình chữ nhật

Suy ra: \(AK=FE\left(3\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:

\(AE\cdot AB=AK^2\left(4\right)\)

Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)

c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)

\(=AK^2+AK^2+AK^2\)

\(=3\cdot AK^2=3\cdot FE^2\)

2c:

\(\dfrac{1}{\sqrt{5}-2}+\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}-\dfrac{1}{2+\sqrt{5}}\)

\(=\dfrac{2+\sqrt{5}-\sqrt{5}+2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}+\dfrac{\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}\)

\(=\dfrac{4}{5-4}+\sqrt{6}=4+\sqrt{6}\)

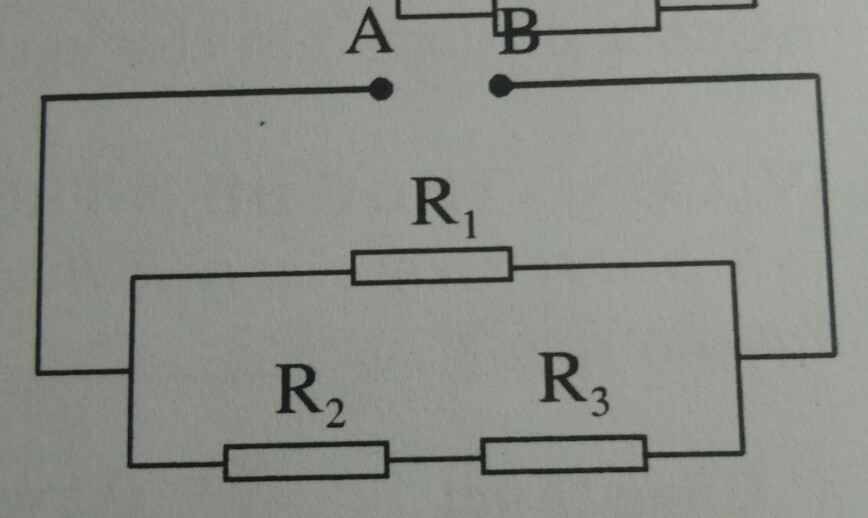
\(a.R_{tđ}=\dfrac{R_1.\left(R_2+R_3\right)}{R_1+R_2+R_3}=\dfrac{6.\left(2+4\right)}{6+2+4}=3\Omega\\ b.U_{AB}=I.R_{tđ}=2.3=6V\\ c.Vì.R_1//R_{23}\Rightarrow U_{AB}=U_1=U_{23}=6V\\ I_1=\dfrac{U_1}{R_1}=\dfrac{6}{6}=1A\\ I_{23}=I-I_1=2-1=1A\\ Vì.R_2ntR_3\Rightarrow I_{23}=I_2=I_3=1A\)

a: Xét (O) có

MA là tiếp tuyến

MB là tiếp tuyến

Do đó: MA=MB

hay M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

nên O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra OM⊥AB

\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)

Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)

Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)

\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)

Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)

a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:

\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)

c) A = x.M + (4x + 7)/(√x + 3)

= 3x/(√x + 3) + (4x + 7)/(√x + 3)

= (7x + 7)/(√x + 3)

Để A nhỏ nhất thì 7x + 7 nhỏ nhất

Mà x ≥ 0

⇒ 7x + 7 ≥ 7

⇒ GTNN của A là 7/3 khi x = 0