ho tam giác ABC vuông tại A có BC=2AB gọi M là trung điểm của BC nối A vói M trên tia đối của tia MA lấy diểm k sao choAM=MK
a, chứng minh tứ giac ABKC là hình chữ nhật
b, gọi E là trung điểm của AM ,F là tung diểm của đối xứng với B qua E chứng minh tứ giác ABMF là hình thoi
c, chứng minh MF//CK
giúp em với ạ




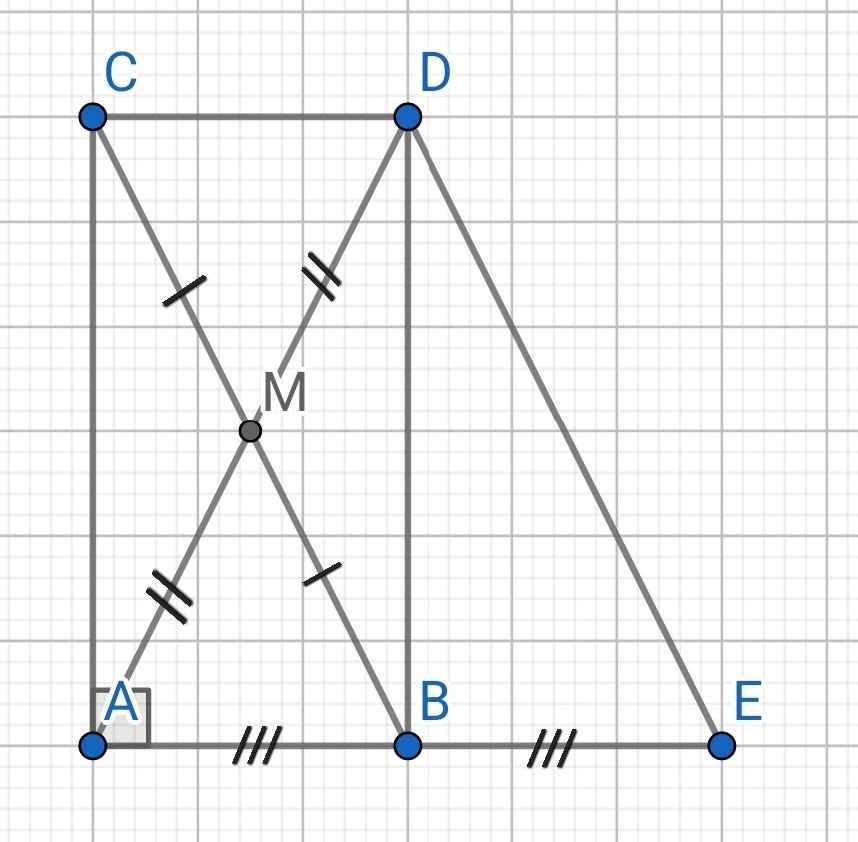
a: Xét tứ giác ABKC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AK
Do đó: ABKC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABKC là hình chữ nhật