giúp bn cái j

Có 2 bài mình vừa đăng đó, các bạn làm được bài nào làm giúp mình với. hhuhu

1) Ta có: \(\dfrac{1}{3x-2}-\dfrac{1}{3x+2}-\dfrac{3x-6}{4-9x^2}\)

\(=\dfrac{3x+2-3x+2+3x-6}{\left(3x-2\right)\left(3x+2\right)}\)

\(=\dfrac{3x-2}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{1}{3x+2}\)

Còn các câu kia nữa ạ !

\(a,\left\{{}\begin{matrix}AB=CD\\AD=BC\\AC\text{ chung}\end{matrix}\right.\Rightarrow\Delta ACB=\Delta CAD\left(c.c.c\right)\\ b,\Delta ACB=\Delta CAD\\ \Rightarrow\widehat{BAC}=\widehat{DCA}\\ \text{Mà 2 góc này ở vị trí so le trong nên }AB\text{//}CD\\ c,\Delta ACB=\Delta CAD\\ \Rightarrow\widehat{BCA}=\widehat{DAC}\\ \text{Mà 2 góc này ở vị trí slt nên }AD\text{//}BC\)

thanks

Bài 1:

\(a,m_{NaOH}=0,2.40=8(g)\\ b,m_{H_2O}=1,5.18=27(g)\)

Bài 2:

\(a,V_{O_2}=0,3.22,4=6,72(l)\\ b,V_{Cl_2}=2.22,4=44,8(l)\)

Bài 3:

\(a,n_{Cu}=\dfrac{6,4}{64}=0,1(mol)\\ b,n_{H_2}=\dfrac{4,48}{22,4}=0,2(mol)\)

Bài 2: 

Xét ΔABC có

AM là đường trung tuyến

AM=BC/2

Do đó: ΔABC vuông tại A

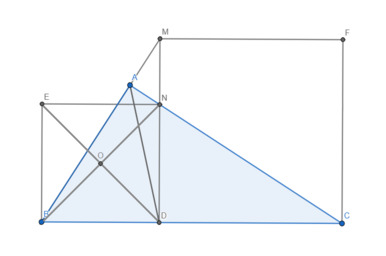
a) ΔABC có AD là phân giác

⇒ \(\dfrac{BD}{AB}\) = \(\dfrac{CD}{AC}\)

ΔDNC đd với ΔABC (g.g) ⇒ \(\dfrac{DN}{AB}\) = \(\dfrac{CD}{AC}\)

⇒ \(\dfrac{BD}{AB}\) = \(\dfrac{DN}{AB}\)

⇒ BD = DN     (đpcm)

b) Gọi O là giao điểm của BN và ED

Chứng minh được BDNE là hình chữ nhật

⇒ BN = ED; O là trung điểm của BN, ED

ΔABN vuông tại A có AO là trung tuyến

⇒ AO = \(\dfrac{1}{2}\).BN

⇒ AO = \(\dfrac{1}{2}\).ED

Mà ΔAED có AO là trung tuyến

⇒ ΔAED vuông tại A

⇒ AE ⊥ AD     (1)

Chứng minh tương tự ta được: AF ⊥ AD     (2)

Từ (1), (2) và theo tiên đề Ơclit

⇒ A, E, F thẳng hàng (đpcm) 

Câu 2.

\(n_{Na_2O}=\dfrac{6,2}{62}=0,1mol\)

\(Na_2O+H_2O\rightarrow2NaOH\)

0,1                           0,2

\(m_{NaOH}=0,2\cdot40=8\left(g\right)\)

\(C\%=\dfrac{8}{6,2+200}\cdot100\%=3,89\%\)

Câu 1.

\(4K+O_2\underrightarrow{t^o}2K_2O\)

\(K_2O+H_2O\rightarrow2KOH\)

\(2KOH+CO_2\rightarrow K_2CO_3+H_2O\)

\(K_2CO_3+BaCl_2\rightarrow2KCl+BaCO_3\downarrow\)

\(2KCl+2H_2O\rightarrow2KOH+Cl_2+H_2\)

​​\(2KOH+CO_2\rightarrow K_2CO_3+H_2O\)​

​\(K_2CO_3+BaCl_2\rightarrow2KCl+BaCO_3\downarrow\)

Bài 7:

a)

\(A=x\left(2x+1\right)-x^2\left(x+2\right)+x^3-x+3\\ =2x^2+x-x^3-2x^2+x^3-x+3\\ =\left(2x^2-2x^2\right)+\left(x-x\right)+\left(-x^3+x^3\right)+3\\ =3\)

Vậy ..........

b)

\(B=2x\left(x-1\right)-x\left(2x+1\right)-\left(3-3x\right)\\ =2x^2-2x-2x^2-x-3+3x\\ =\left(2x^2-2x\right)+\left(-2x-x+3x\right)-3\\ =-3\)

Vậy ...........

c)

\(C=\left(2x+11\right)\left(3x-5\right)-\left(2x+3\right)\left(3x+7\right)\\ =6x^2-10x+33x-55-\left(6x^2+14x+9x+21\right)\\ =6x^2-10x+33x-55-6x^2-14x-9x-21\\ =\left(6x^2-6x^2\right)+\left(-10x+33x-14x-9x\right)-55-21\\ =-76\)

Vậy .............

d)

\(D=x\left(2x^2-4x+8\right)+12x^2\left(\dfrac{1}{3}-\dfrac{1}{6}x\right)-8x+9\\ =2x^3-4x^2+8x+4x^2-2x^3-8x+9\\ =\left(2x^3-2x^3\right)+\left(-4x^2+4x^2\right)+\left(8x-8x\right)+9\\ =9\)

Vậy ...............

`HaNa♬D`

Bài 7.

\(a,A=x\left(2x+1\right)-x^2\left(x+2\right)+x^3-x+3\)

\(=2x^2+x-x^3-2x^2+x^3-x+3\)

\(=\left(-x^3+x^3\right)+\left(2x^2-2x^2\right)+\left(x-x\right)+3\)

\(=3\)

⇒ Giá trị của A không phụ thuộc vào giá trị của biến

\(b,B=2x\left(x-1\right)-x\left(2x+1\right)-\left(3-3x\right)\)

\(=2x^2-2x-2x^2-x-3+3x\)

\(=\left(2x^2-2x^2\right)+\left(-2x-x+3x\right)-3\)

\(=-3\)

⇒ Giá trị của B không phụ thuộc vào giá trị của biến

\(c,C=\left(2x+11\right)\left(3x-5\right)-\left(2x+3\right)\left(3x+7\right)\)

\(=6x^2-10x+33x-55-\left(6x^2+14x+9x+21\right)\)

\(=6x^2+23x-55-6x^2-23x-21\)

\(=\left(6x^2-6x^2\right)+\left(23x-23x\right)+\left(-55-21\right)\)

\(=-76\)

⇒ Giá trị của C không phụ thuộc vào giá trị của biến

\(d,D=x\left(2x^2-4x+8\right)+12x^2\left(\dfrac{1}{3}-\dfrac{1}{6}x\right)-8x+9\)

\(=2x^3-4x^2+8x+4x^2-2x^3-8x+9\)

\(=\left(2x^3-2x^3\right) +\left(-4x^2+4x^2\right)+\left(8x-8x\right)+9\)

\(=9\)

⇒ Giá trị của D không phụ thuộc vào giá trị của biến

#Urushi