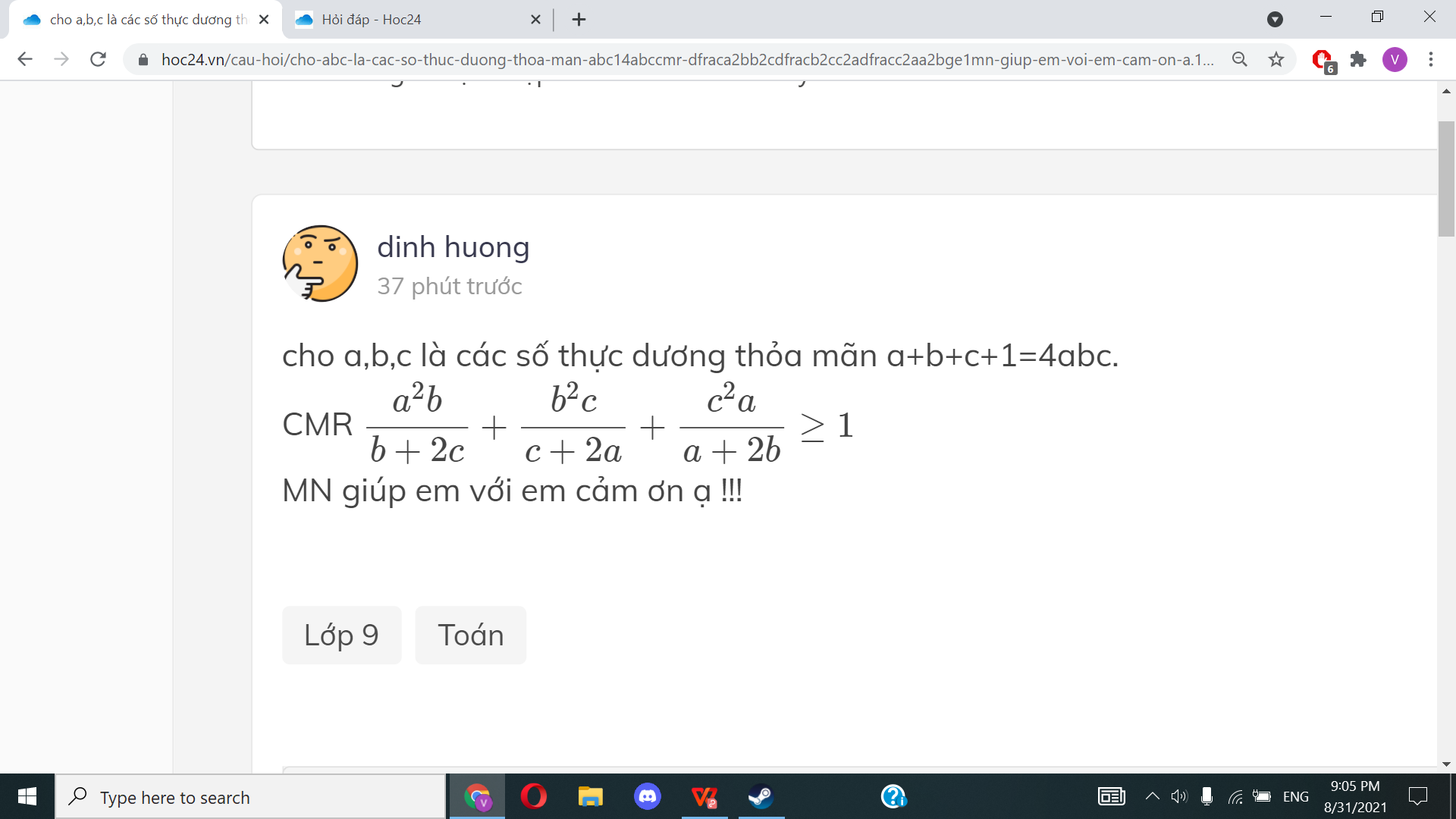
với a,b,c là các số thực dương thỏa mãn a+b+c+1=4abc.CMR
\(\dfrac{a^2b}{b+2c}+\dfrac{b^2c}{c+2a}+\dfrac{c^2a}{a+2b}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
\(\dfrac{a}{a+2b^3}=a-\dfrac{2ab^3}{a+b^3+b^3}\ge a-\dfrac{2ab^3}{3\sqrt[3]{ab^6}}=a-\dfrac{2}{3}.b\sqrt[3]{a^2}\ge a-\dfrac{2}{9}b\left(a+a+1\right)\)
\(\Rightarrow\dfrac{a}{a+2b^3}\ge a-\dfrac{2}{9}\left(2ab+b\right)\)
Tương tự: \(\dfrac{b}{b+2c^3}\ge b-\dfrac{2}{9}\left(2bc+c\right)\) ; \(\dfrac{c}{c+2a^3}\ge c-\dfrac{2}{9}\left(2ac+a\right)\)
Cộng vế:
\(A\ge a+b+c-\dfrac{2}{9}\left(2ab+2bc+2ca+a+b+c\right)=3-\dfrac{2}{9}\left[2\left(ab+bc+ca\right)+3\right]\)
\(A\ge3-\dfrac{2}{9}\left[\dfrac{2}{3}\left(a+b+c\right)^2+3\right]=1\)