cho đồ thị hàm số y=x+1(d1);y=-x+3(d2) và y=mx+m-1(d3)
vẽ d1 và d2 trên cùng mặt phẳng toạ độ
vẽ toạ độ giao điểm của 2 đuờng thẳng (d1) và (d2)
tìm m để (d1) cắt d3 tại trục tung
tìm giá trị của m để ba đường thẳng trên đồng quy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Thay x=4 vào (d1), ta được:
\(y=\dfrac{1}{2}\cdot4=2\)
Vì (d3)//(d2) nên a=-1
Vậy: (d3): y=-x+b
Thay x=2 và y=4 vào (d3), ta được:
b-2=4
hay b=6

a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0
=>m>1
Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0
=>m<1
b: Thay m=3 vào (d), ta được:
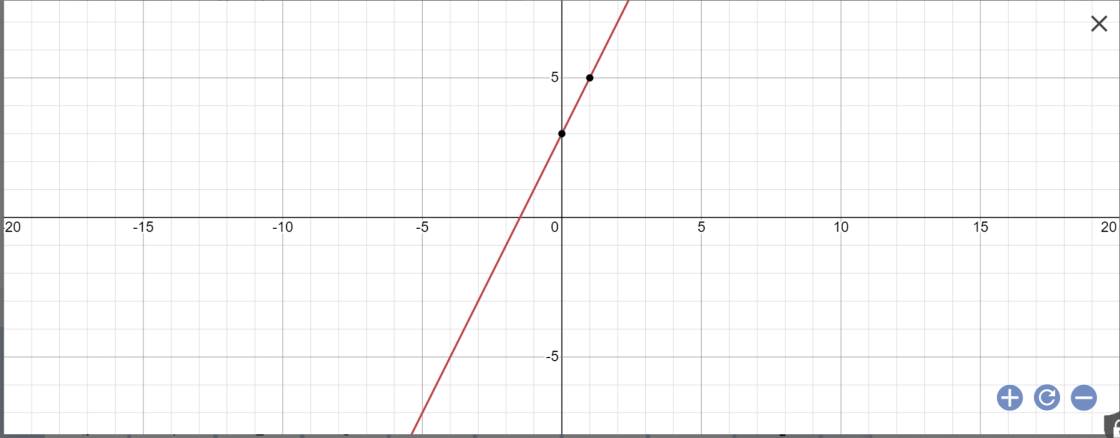
\(y=\left(3-1\right)x+3=2x+3\)
Vẽ đồ thị:
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m-1=2
=>m=3
d: Thay x=-2 và y=0 vào (d1), ta được:
\(-2\left(m-1\right)+3=0\)
=>-2(m-1)=-3
=>\(m-1=\dfrac{3}{2}\)
=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)

a) Tập xác định của hàm số R
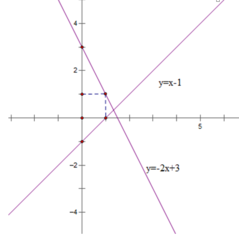
Bảng giá trị
| x | 0 | 1 |
| y = -2x + 3 | 3 | 1 |
| x | 0 | 1 |
| y = x – 1 | - 1 | 0 |

\(b,\left(d_3\right)//\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne-1\end{matrix}\right.\left(1\right)\\ M\left(1;3\right)\in\left(d_3\right)\Leftrightarrow a+b=3\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Vậy \(\left(d_3\right):y=x+2\)
(d1): Cho x = 0 A(0,0) B(1,2) 1 2 C -1 D => y= 0 - A(0,0)
x = 1 => y = 2 - B(1,2)
(d2): Cho x= 0 => y= -1 -C(0,-1)
x = 1 => y = 0 - D(1,0)

b, PT hoành độ giao điểm là \(2x-1=-x+5\Leftrightarrow3x=6\Leftrightarrow x=2\Leftrightarrow y=3\)
\(\Leftrightarrow A\left(2;3\right)\)
Vậy A(2;3) là tọa độ giao điểm 2 đths
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
c: Để (d1) và (d3) cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}m-1=1\\m< >1\end{matrix}\right.\Leftrightarrow m=2\)
d: Thay x=1 và y=2 vào (d3), ta được:
\(m+m-1=2\)
=>2m-1=2
hay m=3/2