cho tam giác ABC vuông tại A, M là trung điểm của BC. trên tia đối của tia MA lấy điểm E sao cho ME = MA
a) chứng minh tam giác AMB = tam giác EMC
b) chứng minh EC vuông góc với AC
c) đường thẳng qua A và song song với đường thẳng BC cắt tia EC ở F. chứng minh C là trung điểm của EF

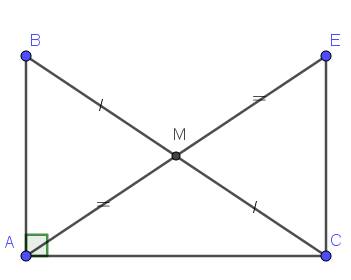
a. Xét \(\Delta AMB\) và \(\Delta EMC\) có:
MA = ME (GT)
\(\widehat{M_1}=\widehat{M_2}\)
BM = MC ( M là trung điểm BC)
\(\Rightarrow\Delta AMB=\Delta EMC\)
b) Ta có \(\Delta AMB=\Delta EMC\Rightarrow\widehat{B}=\widehat{C_1}\) (2 góc tương ứng)
Mà \(\widehat{B}+\widehat{C}=90^0\) (2 góc nhọn tam giác vuông)
\(\Rightarrow\widehat{C}+\widehat{C_1}=90^0\Rightarrow\widehat{ACE}=90^0\Rightarrow CE\perp AC\)
c) Vì \(EC\perp AC\Rightarrow\widehat{C_2}=90^0=\widehat{A}\left(1\right)\)
vì \(AF\) song song BC \(\Rightarrow\widehat{A_1}=\widehat{C}\left(2\right)\) (so le trong)
AC = CA (3)
từ (1) (2) (3) => \(\Delta ABC=\Delta CAF\left(g.c.g\right)\)
\(\Rightarrow AB=CF\) (2 cạnh tương ứng)