Mọi người giúp mìn tính chỗ khoanh : độ lớn cường độ điện trường là cực đại được ko mn, đây là bài lí nhưng phần rút này dùng toán học, nên mình gửi ở trang toán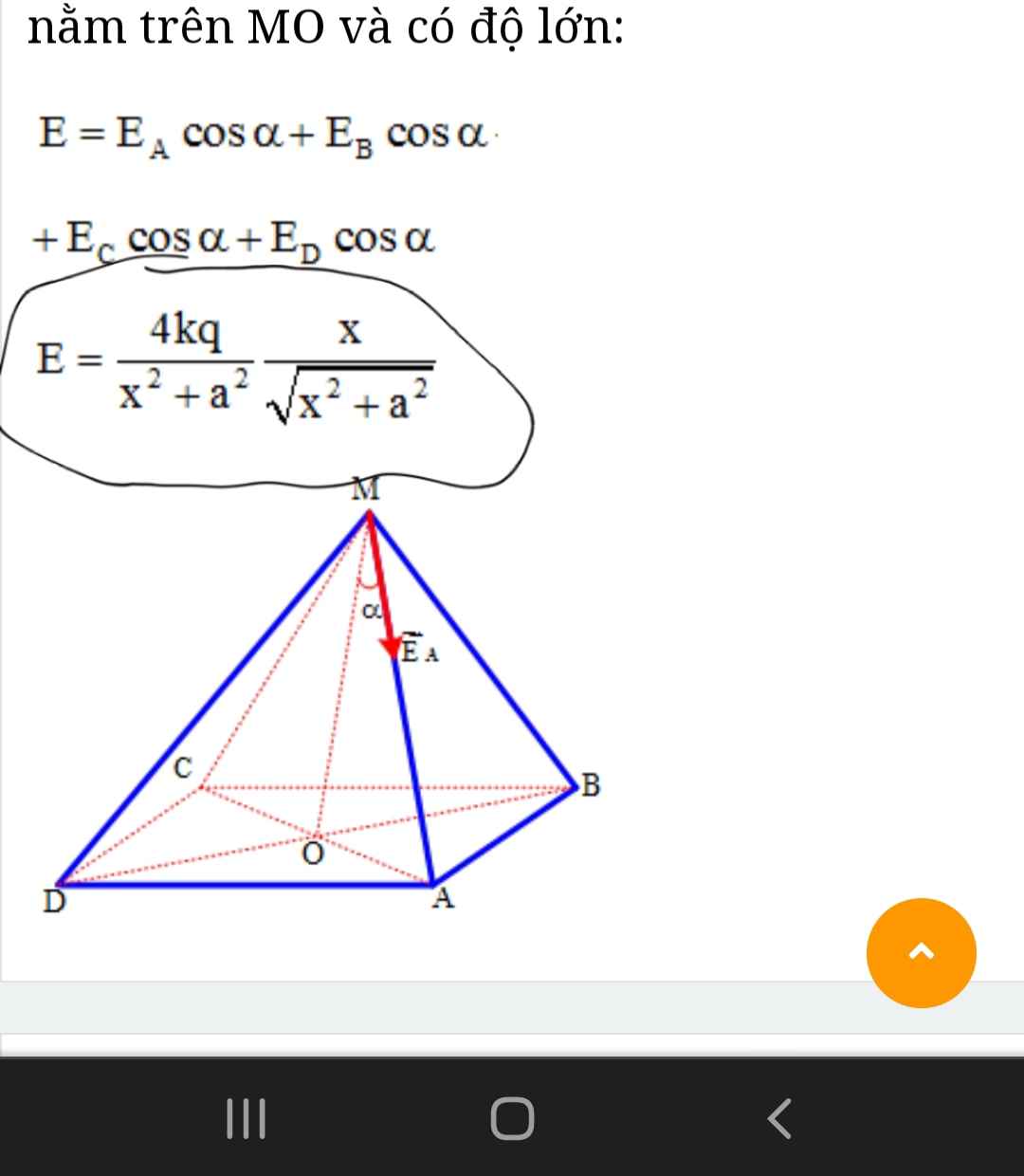
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1> - Những loại thước đo độ dài mà em biết là: thước dây, thước thẳng, thước cuộn, thước kẻ, thước kẹp,...
- Người ta sản xuất ra nhiều loại thước khác nhau như vậy để có thể chọn thước phù hợp với hình dạng, kích thước của vật cần đo.
Ví dụ:
+ Sử dụng thước dây để đo theo hình dạng của vật: đo vòng miệng ngoài cốc, đo cơ thể người, …
+ Sử dụng thước cuộn để đo những độ dài lớn như: chiều cao người, chiều dai lớp học…
+ Sử dụng thước thẳng để đo những độ dài nhỏ, được dùng trong học tập…
2> Dụng cụ mà em có là thước cuộn để đo độ dài sân trường. Thước cuộn có GHĐ là 5m và ĐCNN là 1cm. Cách đo và giá trị trung bình của các kết quả đo trong tổ của em được thực hành trên lớp.
- Cách đo :
+ Độ dài sân trường em khoảng 50m. Đặt thước dọc theo chiều dài sân trường sao cho 1 đầu sân trường ngang bằng với vạch số 0 của thước.
+ Đặt mắt nhìn theo hướng vuông góc với cạnh thước.
+ Đọc và ghi kết quả đo theo vạch chia gần nhất với đầu kia của vật.
+ Đo khoảng 10 lần thì mới hết chiều dài sân trường và cộng kết quả 10 lần đo.
+ Thay phiên nhau các bạn trong tổ đo lại chiều dài. Đo chiều dài sân trường 3 lần rồi lấy kết quả 3 lần đo cộng lại chia 3 thì ra kết quả trung bình.

mình thấy là như này :
mik thì ik trả lời , làm bài -> các bn ý chọn thì chọn thì chọn kg thì thôi ( giúp )
còn mấy bn 2000- 3000
chác biết kiếm đâu ra chằng bao giờ thấy trả lời nhưng lại đứng đc trong bảng xếp hạng ???

Đáp án D
Cách giải:
+ Trong mạch dao động LC thì cường độ điện trường E trong tụ biến thiên vuông pha với cảm ứng từ B trong lòng ống dây. Khi E = 0,5E0 thì
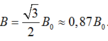

Đúng thì xin k sai thì thôi
a) Học nhóm rất thú vị.
b) Các bạn thảo luận dở quá.
c) Cậu hát rất hay!
d) Các bạn ấy chơi vui quá!

Rút chỉ còn (m.(kq))/a^2 thoy nha mn, m là phần số í
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)