a) Xét tứ giác ADME có 

ME//AD(gt)

MD//AE(gt)

Do đó: ADME là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Hình bình hành ADME có \(\widehat{EAD}=90^0\)(\(\widehat{BAC}=90^0,E\in AC,D\in AB\))

nên ADME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

b) Ta có: ADME là hình chữ nhật(cmt)

nên ED=AM(Hai đường chéo trong hình chữ nhật ADME)

mà ED=5cm(gt)

nên AM=5cm

Ta có: ΔABC vuông tại A(gt)

mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)

nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

\(\Leftrightarrow BC=2\cdot AM=2\cdot5=10\left(cm\right)\)

Xét ΔABC có AH là đường cao ứng với cạnh BC(gt)

nên \(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{4.8\cdot10}{2}=24\left(cm^2\right)\)

c) Xét ΔABC có 

M là trung điểm của BC(gt)

ME//AB(gt)

Do đó: E là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)

Xét ΔABC có 

M là trung điểm của BC(gt)

MD//AC(gt)

Do đó: D là trung điểm của AB(Định lí 1 về đường trung bình của tam giác)

Ta có: ΔAHB vuông tại H(AH⊥BC tại H)

mà HD là đường trung tuyến ứng với cạnh huyền AB(D là trung điểm của AB)

nên \(HD=\dfrac{AB}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

mà \(AD=\dfrac{AB}{2}\)(D là trung điểm của AB)

nên HD=AD

Ta có: ΔAHC vuông tại H(AH⊥BC tại H)

mà HE là đường trung tuyến ứng với cạnh huyền AC(E là trung điểm của AC)

nên \(HE=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

mà \(AE=\dfrac{AC}{2}\)(E là trung điểm của AC)

nên HE=AE

Xét ΔEAD và ΔEHD có 

EA=EH(cmt)

ED chung

AD=HD(cmt)

Do đó: ΔEAD=ΔEHD(c-c-c)

⇒\(\widehat{EAD}=\widehat{EHD}\)(hai góc tương ứng)

mà \(\widehat{EAD}=90^0\)(\(\widehat{BAC}=90^0\), D∈AB, E∈AC)

nên \(\widehat{EHD}=90^0\)

hay HD⊥HE(đpcm)

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

=>ΔABC đồng dạng với ΔHBA

b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

HB=6^2/10=3,6cm

a: BC=căn 3^2+4^2=5cm

AB<AC<BC

=>góc C<góc B<góc A

c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>DA=DE

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

góc ADF=góc EDC

=>ΔDAF=ΔDEC

a: BC=căn 3^2+4^2=5cm

b,d: Đề bài yêu cầu gì?

c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>DA=DE

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

góc ADF=góc EDC

=>ΔDAF=ΔDEC

làm j có tam giác nào cân tại A ( A<90^o)

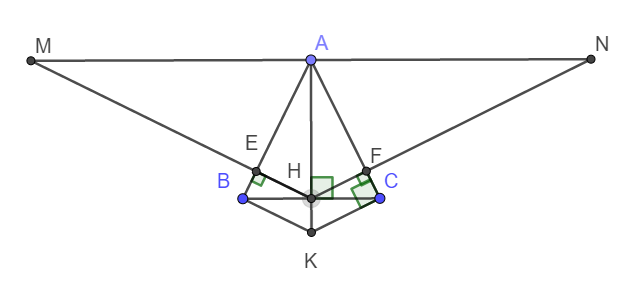
a) Xét tam giác vuông ABH và tam giác vuông ACH có:

Cạnh AH chung

AB = AC (gt)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)  (Hai góc tương ứng)

Vậy nên AH là tia phân giác góc BAC.

b) Xét hai tam giác vuông AEH và AFH có:

Cạnh AH chung

\(\widehat{EAH}=\widehat{FAH}\)

\(\Rightarrow\Delta AEH=\Delta AFH\)  (Cạnh huyền - góc nhọn)

\(\Rightarrow HE=HF\)  (Hai cạnh tương ứng)

Suy ra tam giác HEF cân tại E.

c) Dễ thấy \(\Delta ABK=\Delta ACK\left(c-g-c\right)\)

\(\Rightarrow\widehat{AKB}=\widehat{AKC}\)

Lại có \(\widehat{AKC}=\widehat{AHF}\)   (Đồng vị) 

\(\widehat{AHF}=\widehat{AHE}\) (Do \(\Delta AEH=\Delta AFH\) )

\(\Rightarrow\widehat{AKB}=\widehat{AHE}\) hay HE // BK

d) Ta có \(\Delta AHN=\Delta AHM\left(c-g-c\right)\)

\(\Rightarrow\widehat{MAH}=\widehat{NAH}=90^o\)

\(\Rightarrow\widehat{MAN}=180^o\) hay M, N, A thẳng hàng.