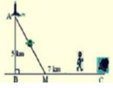
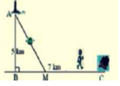
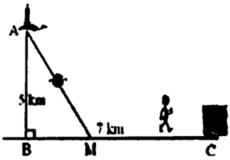
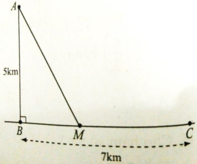
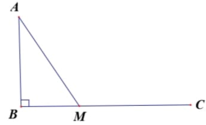
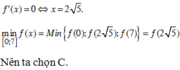Một ngọn hải đăng đặt ở vị trí A có khoảng cách đến bờ biển là AB=4km. Trên bờ biển có 1 cái kho đặt ở vị trí C cách B một khoảng 5km. Một người chèo thuyền từ A đến vị trí M trên bờ biển giữa B và C, đường đi của thuyền tạo với bờ biển BC một góc xấp xỉ 530. Hỏi sau bao lâu người đó đến được C, biết vận tốc thuyền đi từ A đến M là 5km/h và đi bộ từ M đến C vận tốc đi bộ là 6km/h
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
Đặt BM= x , CM =7-x-> A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
Đặt BM= x , CM =7-x ⇒ A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

Đáp án A
Phương pháp: Sử dụng phương pháp hàm số.
Cách giải: Gọi độ dài đoạn MB là x ![]()
Tam giác ABM vuông tại B => ![]()
Thời gian người đó đi từ A tới C: 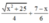
Xét hàm số f(x) 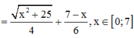

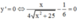
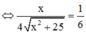
![]()
![]()
=> x = 2 5
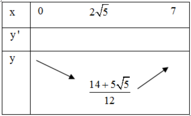
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là 2 5

Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 - x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có
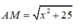
Thời gian đi từ A đến M là
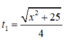
thời gian đi từ M đến C là
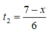
Tổng thời gian đi từ A đến C là
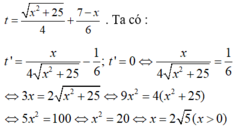
Bảng biến thiên
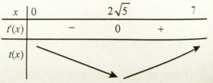
Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2√5 ≈ 4,5
Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.
Chọn B

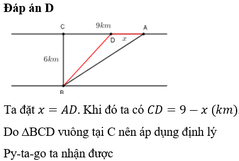
Đáp án B
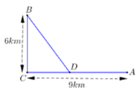
Đặt A D = x → C D = 9 − x suy ra B D = 9 − x 2 + 36 km
Chi phí lắp đặt trên đoạn AD (trên bờ) là T 1 = 100 x triệu đồng
Chi phí lắp đặt trên đoạn DB (dưới nước) là T 2 = 260 9 − x 2 + 36 triệu đồng
Vậy tổng chi phí cần tính là T = T 1 + T 2 = 100 x + 260 9 − x 2 + 36 → f x
Xét hàm số f x = 100 x + 260 x 2 − 18 x + 117 trên đoạn 0 ; 9 → min 0 ; 9 f x = 2340
Dấu = xảy ra khi và chỉ khi x = 13 2 = 6 , 5 km

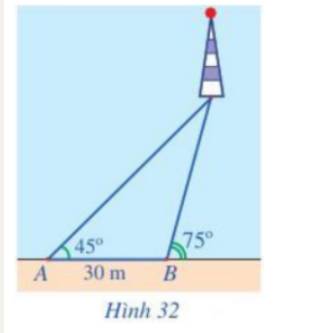
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
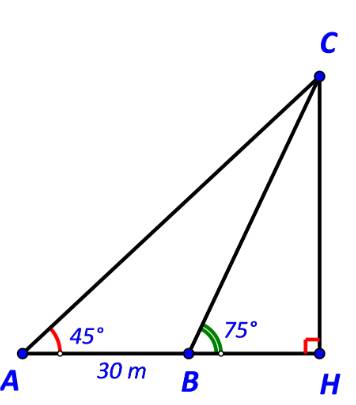
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.