tìm bộ 3 số nguyên dương (x;y;z) thỏa mãn x3+y3+3xyz=z3=2(2x+2y)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2019
1,https://diendantoanhoc.net/topic/157361-t%C3%ACm-c%C3%A1c-s%E1%BB%91-nguy%C3%AAn-x-y-tho%E1%BA%A3-m%C3%A3n-x3y32016/
NK
1
18 tháng 11 2016
Trả lời hộ mik đi các bn, trả lời xong mik kik cho
27 tháng 7 2015
abc=a^3+b^3+c^3=(a+b+c)(a+b+c)(a+b+c)
mà số nguyên dương nhỏ nhất ^ ba là 125 nên a+b+c=5(ko thỏa mãn)
__________________nhỏ hai_______216 nên a+b+c=6(ko thỏa mãn)
______________________ba________343 _________7___________
______________________tư________512_________(thỏa mãn)
_____________________năm_______729________9(ko thỏa mãn)
Vậy chỉ có 1 và chỉ 1 số nguyên dương có 3 chữ số abc thỏa mãn đề là: 512
mk ko biết tại sao thử máy tính k đúng, nhưng bạn có thể vận dụng cách của mk, hình như mk sai chỗ phân tích a^3+b^3+c^3
đừng **** nhá,
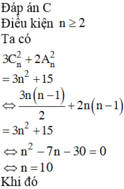
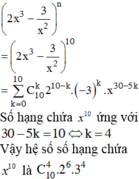
Lời giải:
Áp dụng công thức hằng đẳng thức:
\(x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-xz)\) ta có:
\(x^3+y^3+3xyz=z^3\)
\(\Leftrightarrow x^3+y^3+(-z)^3-3xy(-z)=0\)
\(\Leftrightarrow (x+y-z)(x^2+y^2+z^2-xy+xz+yz)=0\)
TH1: \(x+y-z=0\)
\(\Leftrightarrow z=x+y\)
Thay vào: \(z^3=2(2x+2y)^2=8(x+y)^2\)
\(\Leftrightarrow (x+y)^3=8(x+y)^2\)
\(\Leftrightarrow (x+y)^2(x+y-8)=0\)
Do x,y nguyên dương nên \((x+y)^2\neq 0\Rightarrow x+y-8=0\Rightarrow x+y=8\Rightarrow z=8\)
\(x+y=8\Rightarrow (x,y)=(1,7); (2;6); (3;5); (4;4)\) và các hoán vị tương ứng
TH2: \(x^2+y^2+z^2-xy+yz+xz=0\)
\(\Leftrightarrow \frac{(x-y)^2+(y+z)^2+(z+x)^2}{2}=0\)
Vì \((x-y)^2; (y+z)^2; (z+x)^2\geq 0\Rightarrow (x-y)^2+(y+z)^2+(x+z)^2\geq 0\)
Dấu bằng xảy ra khi \(\left\{\begin{matrix} x-y=0\\ y+z=0\\ z+x=0\end{matrix}\right.\) (vô lý do x,y,z nguyên dương)
Vậy \((x,y,z)=(1;7;8); (2;6;8); (3;5;8); (4;4;8); (5;3;8); (6;2;8); (7;1;8)\)