Cho hai đường thẳng (d1): y = (2 + m)x + 1 và (d2): y = (1 + 2m)x + 2
a, tìm m để d1 và d2 cắt nhau
b, với m = -1 , vẽ (d1)và (d2)trên mặt phẳng tọa độ Oxy rồi tìm toạ độ giao điểm của hai đường thẳng(d1) và (d2) bằng phép tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Để hai đường thẳng cắt nhau thì
2m+1<>m+2
hay m<>1

\(d_1:mx+y=3m-1.\\ \Leftrightarrow-mx+3m-1=y.\)
\(d_2:x+my=m+1.\\ \Leftrightarrow my=-x+m+1.\\\Leftrightarrow y=\dfrac{-x}{m}+\dfrac{m}{m}+\dfrac{1}{m}.\Leftrightarrow y=-\dfrac{1}{m}x+1+\dfrac{1}{m}.\)
Thay m = 2 vào phương trình đường thẳng d1 ta có:
\(-2x+3.2-1=y.\\ \Leftrightarrow-2x+5=y.\)
Thay m = 2 vào phương trình đường thẳng d2 ta có:
\(y=-\dfrac{1}{2}x+1+\dfrac{1}{2}.\\ \Leftrightarrow y=\dfrac{-1}{2}x+\dfrac{3}{2}.\)
Xét phương trình hoành độ giao điểm của d1 và d2 ta có:
\(-2x+5=\dfrac{-1}{2}x+\dfrac{3}{2}.\\ \Leftrightarrow\dfrac{-3}{2}x=-\dfrac{7}{2}.\\ \Leftrightarrow x=\dfrac{7}{3}.\)
\(\Rightarrow y=\dfrac{1}{3}.\)
Tọa độ giao điểm của d1 và d2 khi m = 2 là \(\left(\dfrac{7}{3};\dfrac{1}{3}\right).\)

a) để \(\left(d_1\right)\cap\left(d_2\right)\) thì \(\left(2+m\right)x+1=\left(1+2m\right)x+2\)
\(\Leftrightarrow2x+mx+1=x+2mx+2\Leftrightarrow mx=x-1\Leftrightarrow m=\dfrac{x-1}{x}\)
b) bn tự vẽ nha :)
thế \(m=-1\) vào \(\left(d_1\right);\left(d_2\right)\) ta có : \(\left(d_1\right):y=x+1;\left(d_2\right):-x+2\)
để \(\left(d_1\right)\cap\left(d_2\right)\Leftrightarrow x+1=-x+2\Leftrightarrow x=\dfrac{1}{2}\) \(\Rightarrow y=\dfrac{1}{2}+1=\dfrac{3}{2}\)
\(\Rightarrow\left(d_1\right)\cap\left(d_2\right)\) tại \(A\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)

Với m = 2 thì d 1 : y = 2x + 3; d 2 : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
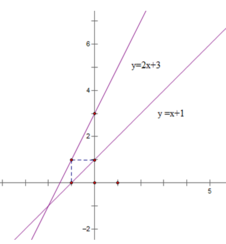
Gọi A ( x 0 ; y 0 ) là tọa độ giao điểm của d1 và d2
Khi đó:
( y 0 = 2 x 0 + 3 và y 0 = x 0 + 1
⇒ 2xo + 3 = x 0 + 1 ⇔ x 0 = -2
⇒ y 0 = x 0 + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d 1 và d 2 là (-2; -1)

a) Để (d1) và (d2) cắt nhau thì:
\(\left\{{}\begin{matrix}m\ne-2\\m\ne\dfrac{-1}{2}\\2+m\ne1+2m\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\m\ne\dfrac{-1}{2}\\m\ne1\end{matrix}\right.\)

a: 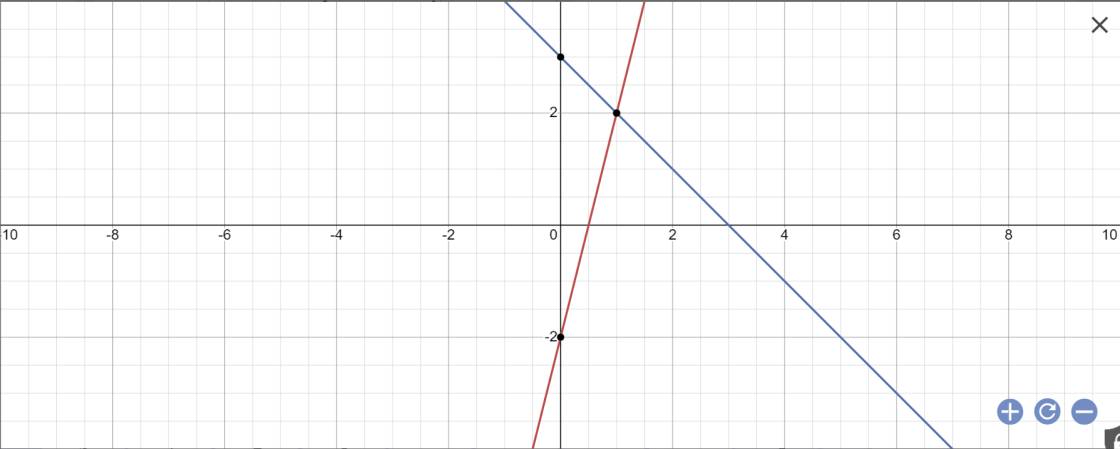
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)

\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)

b: Phương trình hoành độ giao điểm là:
x+1=-x+3
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
hay y=2
a, để d1 cat d2 <=> \(2+m\ne1+2m\)
\(\Leftrightarrow m\ne1\)
b, d1: y= x + 1
d2: y= -x + 2
pt hoanh do giao diem cua d1 va d2:
x+1 = -x +2 <=> x = 1/2
=> y = 1/2 +1 = 1,5
toa đô giao diem A(1/2 ; 1,5)
hìh tụ vẽ
a,\(\left(d_1\right)\cap\left(d_2\right)\Rightarrow a\ne a'\)
=> \(2+m\ne1+2m\)\(\Leftrightarrow m\ne1\)
b, thay m=-1 vào ta được
\(\left(d_1\right):y=1x+1\)
\(\left(d_2\right):y=-x+2\)
Hoành độ giao điểm của 2 đường thẳng là nghiệm của pt:
x+1=-x+2
\(\Leftrightarrow2x=1\Leftrightarrow x=\dfrac{1}{2}\)thay vào \(\left(d_1\right)\) ta có: y=\(\dfrac{1}{2}+1=\dfrac{3}{2}\)
Vậy tọa độ giao điểm của 2 đường thẳng là A\(\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)