Cho hàm số 2x2-4mx-m+5. Có tất cả bao nhiêu giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Nhắc lại quy tắc vẽ đồ thị hàm số y = f x từ đồ thị hàm số y = f x
- Phần 1: Giữ nguyên phần đồ thị hàm số y = f x bên phải trục Oy (bỏ phần bên trái)
- Phần 2: Lấy đối xứng phần đồ thị hàm số y = f x bên phải trục O qua trục O
- Hợp của 2 phần, ta được đồ thị hàm số y = f x
Xét y = f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3 với f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3
Để hàm số y = f x có 5 điểm cực trị ⇔ y = f x có 2 điểm cực trị nằm phía bên phải trục Oy ⇔ f ' x = 0 có 2 nghiệm dương phân biệt ⇔ x 2 − 4 x + m − 1 = 0 có 2 nghiệm dương phân biệt x 1 , x 2
⇔ Δ > 0 x 1 + x 2 > 0 x 1 x 2 > 0 ⇔ 5 − m > 0 m − 1 > 0 ⇔ 1 < m < 5 . Kết hợp m ∈ ℤ → m = 2 ; 3 ; 4

Đáp án C
Xét hàm số f x = x 2 − 2 x + m trên đoạn [-1;2]
Tạ có: f ' x = 2 x − 2 = 0 ⇒ x = 1
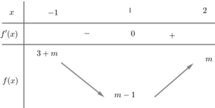
Lại có: f 0 = m ; f − 1 = m − 1 ; f 2 = m + 2
Do đó f x ∈ m − 1 ; m + 2
Nếu m − 1 ≥ 0 ⇒ max 0 ; 2 f x = m + 2 = 5 ⇔ m = 3
Nếu m − 1 < 0 suy ra max 0 ; 2 f x = m + 2 max 0 ; 2 f x = 1 − m
TH1: max 0 ; 2 f x = m + 2 = 5 ⇔ m = 3 k o _ t / m
TH2: max 0 ; 2 f x = 1 − m ⇔ m = − 4 ⇒ m + 1 = − 3 t / m
Vậy m = 3 ; m = − 4 là giá trị cần tìm

\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Để \(g\left(x\right)_{min}>0\Rightarrow f\left(x\right)=0\) vô nghiệm trên đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}-m< -2\\-m>7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -7\end{matrix}\right.\)
\(g\left(0\right)=\left|m-1\right|\) ; \(g\left(1\right)=\left|m-2\right|\) ; \(g\left(2\right)=\left|m+7\right|\)
Khi đó \(g\left(x\right)_{min}=min\left\{g\left(0\right);g\left(1\right);g\left(2\right)\right\}=min\left\{\left|m-2\right|;\left|m+7\right|\right\}\)
TH1: \(g\left(x\right)_{min}=g\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m-2\right|\le\left|m+7\right|\\\left|m-2\right|=2020\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{5}{2}\\\left|m-2\right|=2020\end{matrix}\right.\) \(\Rightarrow m=2022\)
TH2: \(g\left(x\right)_{min}=g\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m+7\right|\le\left|m-2\right|\\\left|m+7\right|=2020\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\dfrac{5}{2}\\\left|m+7\right|=2020\end{matrix}\right.\) \(\Rightarrow m=-2027\)

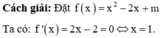

ta có hàm số
\(y=2\left(x^2-2mx+m^2\right)-\left(2m^2+m-5\right)\ge-\left(2m^2+m-5\right)\)
vậy \(-\left(2m^2+m-5\right)=5\Leftrightarrow2m^2+m=0\Leftrightarrow\orbr{\begin{cases}m=0\\m=-\frac{1}{2}\end{cases}}\)
Vậy có hai giá trị của m