Theo bài ra ta có : \(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}\)

\(\Rightarrow\frac{a\left(2bz-3cy\right)}{a^2}=\frac{2b\left(3cx-az\right)}{\left(2b\right)^2}=\frac{3c\left(ay-2bx\right)}{\left(3c\right)^2}\)

\(\Rightarrow\frac{2abz-3acy}{a^2}=\frac{6bcx-2abz}{\left(2b\right)^2}=\frac{3acy-6bcx}{\left(3c\right)^2}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có : 

\(\frac{2abz-3acy}{a^2}=\frac{6bcx-2abz}{\left(2b\right)^2}=\frac{3acy-6bcx}{\left(3c\right)^2}=\frac{2abz-3acy+6bcx-2abz+3acy-6bcx}{a^2+\left(2b\right)^2+\left(3c\right)^2}=0\)

=> \(\hept{\begin{cases}2bz=3cy\\3cx=az\\ay=2bx\end{cases}}\Rightarrow\hept{\begin{cases}\frac{z}{3c}=\frac{y}{2b}\\\frac{z}{3c}=\frac{x}{a}\\\frac{y}{2b}=\frac{x}{a}\end{cases}\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}\left(\text{đpcm}\right)}\)

đây nhé bạn

fraction{320}{3}

Câu hỏi
# Cho dãy tỉ số bằng nhau ( 2bz-3cy )/a=(3cx az)/2b=(ay-2bx)/3c. Chứng minh: x/a=y/2b=z/3c.
Trả lời
Đáp án:+Giải thích các bước giải:


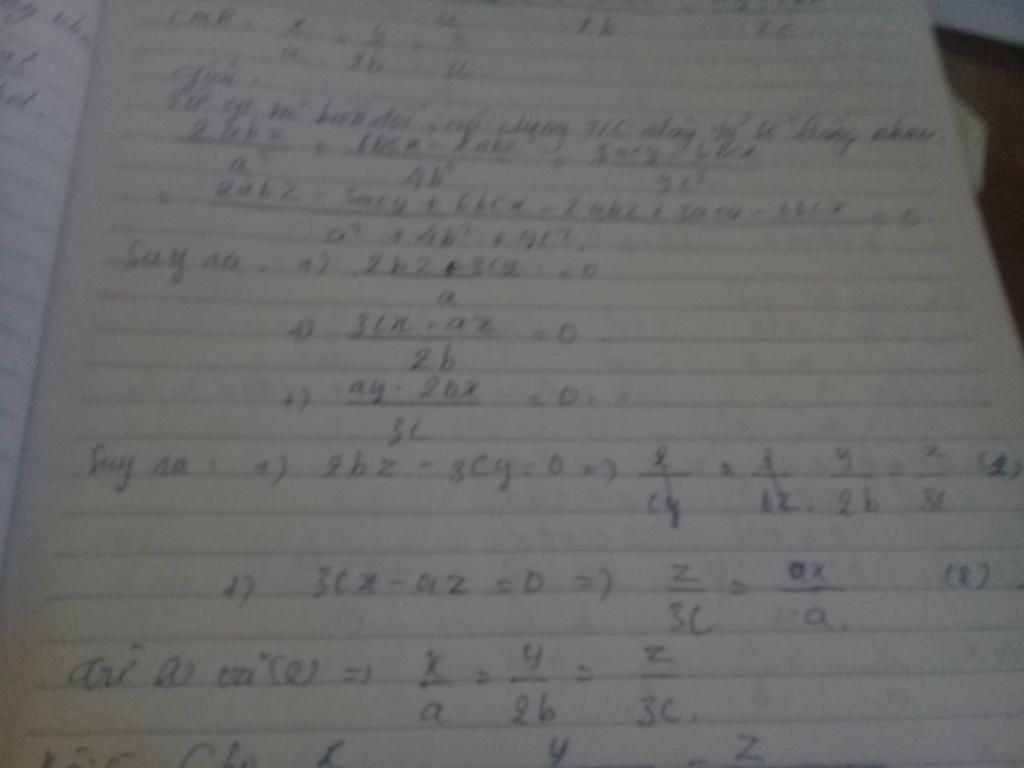
bạn tìm trên link này nhá mk ko gửi hình ảnh đc

Ta có : \(\dfrac{2bz-3cy}{a}=\dfrac{3cx-az}{2b}=\dfrac{ay-2bx}{3c}\)

=> \(\dfrac{\left(2bz-3cy\right)a}{a^2}=\dfrac{\left(3cx-az\right)2b}{4b^2}=\dfrac{\left(ay-2bx\right)3c}{9c^2}\)

\(\dfrac{2bza-3cya}{a^2}=\dfrac{6cxb-2bza}{4b^2}=\dfrac{3cya-6cxb}{9c^2}\)

Áp dụng t/c dãy tỉ số bằng nhau :

\(\dfrac{2bza-3cya}{a^2}=\dfrac{6cxb-2bza}{4b^2}=\dfrac{3cya-6cxb}{9c^2}=\dfrac{2bza-3cya+6xb-2bza+3cya-6cxb}{a^2+4b^2+9c^2}=\dfrac{0}{a^2+4b^2+9c^2}=0\)Ta có : \(\dfrac{2bza-3cya}{a^2}=0\)

=> 2bza - 3cya = 0

=> 2bza = 3cya

=> \(\dfrac{y}{2b}=\dfrac{z}{3c}\) (1)

Ta có : \(\dfrac{6cxb-2bza}{4b^2}=0\)

=> 6cxb - 2bza = 0

=> 6cxb = 2bza

=> 3cx = za

=> \(\dfrac{z}{3c}=\dfrac{x}{a}\) (2)

Từ (1),(2) => \(\dfrac{x}{a}=\dfrac{y}{2b}=\dfrac{z}{3c}\) (ĐPCM)

Ta có: \(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}.\)

\(\Rightarrow\frac{a.\left(2bz-3cy\right)}{a^2}=\frac{2b.\left(3cx-az\right)}{4b^2}=\frac{3c.\left(ay-2bx\right)}{9c^2}.\)

\(\Rightarrow\frac{2abz-3acy}{a^2}=\frac{6bcx-2abz}{4b^2}=\frac{3acy-6bcx}{9c^2}.\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được:

\(\frac{2abz-3acy}{a^2}=\frac{6bcx-2abz}{4b^2}=\frac{3acy-6bcx}{9c^2}=\frac{2abz-3acy+6bcx-2abz+3acy-6bcx}{a^2+4b^2+9c^2}=\frac{\left(2abz-2abz\right)-\left(3acy-3acy\right)+\left(6bcx-6bcx\right)}{a^2+4b^2+9c^2}=0.\)

\(\Rightarrow\left\{{}\begin{matrix}\frac{2bz-3cy}{a}=0\\\frac{3cx-az}{2b}=0\\\frac{ay-2bx}{3c}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2bz-3cy=0\\3cx-az=0\\ay-2bx=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2bz=3cy\\3cx=az\\ay=2bx\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\frac{z}{3c}=\frac{y}{2b}\\\frac{x}{a}=\frac{z}{3c}\\\frac{y}{2b}=\frac{x}{a}\end{matrix}\right.\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}\left(đpcm\right).\)

Chúc bạn học tốt!

Mình mới học lóp 6

Bạn không làm đc thì thui có ai khiến bạn trả lời lớp mấy đâu