Hóng ké ai đó giải bài nì, ko thì toi xách mông đi hỏi, ngu hình quá :(

vậy thì bạn ấn theo dõi bài này là đc mà, bạn bình luận vậy lỡ có ai tưởng có người trả lời rồi nên không giúp ;_;

Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).

\( \Rightarrow SO \bot \left( {ABC} \right)\)

Tam giác \(ABC\) đều

\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)

Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}}  = \frac{{a\sqrt 6 }}{3}\)

\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)

Chọn đáp án D

Gọi M,N lần lượt là trung điểm AB, CD

Đáp án B

Cách giải:

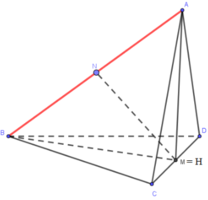
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD)) ⇒ H ∈ BM, AH ⊥ HM

VABCD lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M

Hai tam giác ACD, BCD đều, cạnh a, có đường cao AM, BM bằng  a 3 2

Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB ⇒ MN ⊥ AB

Mà MN ⊂ (AMB) ⊥ CD ⇒ MN ⊥ CD ⇒ MN là đoạn vuông góc chung của AB và CD

Khoảng cách giữa hai đường thẳng AB và CD là:

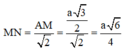
1.

Gọi $I$ là trung điểm $AB$ thì do tam giác $DAB$ và $CAB$ cân tại $D$ và $C$ nên:

$DI\perp AB; CI\perp AB$

$\Rightarrow (DCI)\perp AB$

$\Rightarrow (DCI)\perp AI$ và $(DCI)\perp BI$

Do đó:

\(V_{ABCD}=V_{DAIC}+V_{DIBC}=\frac{1}{3}AI.S_{DIC}+\frac{1}{3}BI.S_{DIC}\)

\(=\frac{1}{3}S_{DIC}(AI+BI)=\frac{1}{3}S_{DIC}.AB=\frac{x}{3}S_{DIC}\)

\(DI=\sqrt{DA^2-AI^2}=\sqrt{DA^2-(\frac{AB}{2})^2}=\sqrt{12-\frac{x^2}{4}}\)

\(CI=\sqrt{AC^2-AI^2}=\sqrt{AC^2-(\frac{AB}{2})^2}=\sqrt{12-\frac{x^2}{4}}\)

$\Rightarrow DCI$ là tam giác cân tại $I$

Kẻ $IM\perp DC$ thì $M$ là trung điểm $DC$

$IM=\sqrt{DI^2-DM^2}=\sqrt{12-\frac{x^2}{4}-(\sqrt{3})^2}$

$=\sqrt{9-\frac{x^2}{4}}$

\(S_{DIC}=\frac{IM.DC}{2}=\sqrt{9-\frac{x^2}{4}}.2\sqrt{3}:2=\frac{\sqrt{3}.\sqrt{36-x^2}}{2}\)

Vậy: \(V_{ABCD}=\frac{\sqrt{3}}{6}x\sqrt{36-x^2}=\frac{\sqrt{3}}{6}\sqrt{x^2(36-x^2)}\)

\(\leq \frac{\sqrt{3}}{6}.\frac{x^2+36-x^2}{2}=3\sqrt{3}\) theo BĐT Cô-si

Vậy $V_{ABCD}$ max bằng $3\sqrt{3}$ khi $x^2=36-x^2$
$\Leftrightarrow x=3\sqrt{2}$

Hình bài 1

A.\(\dfrac{a\sqrt{6}}{3}\)

\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)

\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)

\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)

A

C