Cho hình bình hành ABCCD các đường phân giác của các góc A ; B; C; D cắt nhau tại ra tứ giác HEFG Chứng minh tứ giác HEFG là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


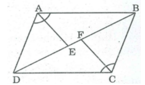
Hình ABCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Hình ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.

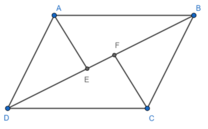
Ta có S A B C F E = S A B E + S B F C S A D C F E = S D F C + S D A E
Xét hình bình hàng ABCD có AE và CF lần lượt là phân giác của các góc A và C
nên suy ra: B A E ^ = D A E ^ = B C F ^ = D C F ^
Xét ΔABE và ΔDCF có:
AB = CD (gt), A B E ^ = C D F ^ (slt), B A E ^ = D C F ^ (cmt)
=> ΔABE = ΔDCF (g.c.g)
=> SABE = SCDF (1)
Xét ΔBCF và ΔDAE có:
AD = BC (gt), A D E ^ = C B F ^ (slt), D A E ^ = B C F ^ (cmt)
=> ΔBCF = ΔDAE (g.c.g)
=> SBCF = SDAE (2)
Từ (1) và (2) suy ra:
SABE + SBCF = SCDF + SDAE
=> SABCFE = SADCFE
Đáp án cần chọn là: C

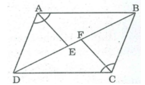
Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E
đề sai rồi