Cho tam giác ABC có AB=AC, M là tr/điểm của BC, từ M kẻ MH⊥AB, AC⊥MK( H thuộc AB, K thuộc AC). Cminh:
a)AM ⊥BC
b)AH=AK
c)HK//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2022
a: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK; AH=AK
b: Xét ΔABC có
AM là đường trung tuyến
AM là đường cao
Do đó: ΔABC cân tại A
DT
20 tháng 3 2019
a, xét tam giác AMB và tam giác AMC có:
AB=AC(gt)
\(\widehat{BAM}\) =\(\widehat{CAM}\)(gt)
AM chung
suy ra tam giác AMB= tam giác AMC(c.g.c)
b,xét tam giác AHM và tam giác AKM có:
AM cạnh chung
\(\widehat{HAM}\)=\(\widehat{KAM}\)(gt)
suy ra tam giác AHM=tam giác AKM(CH-GN)
Suy ra AH=AK
c,gọi I là giao điểm của AM và HK
xét tam giác AIH và tam giác AIK có:
AH=AK(theo câu b)
\(\widehat{IAH}\)=\(\widehat{IAK}\)(gt)
AI chung
suy ra tam giác AIH=tam giác AIK (c.g.c)
Suy ra \(\widehat{AIH}\)=\(\widehat{AIK}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIH}\)=\(\widehat{AIK}\)= 90 độ
\(\Rightarrow\)HK vuông góc vs AM
26 tháng 2 2023
a: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
b: Xet ΔABC có HK//BC
nên AH/AB=HK/BC
=>HK/18=6/9=2/3
=>HK=12(cm)
c: Xét ΔABM có HI//BM
nên HI/BM=AI/AM
Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
=>HI/BM=IK/MC
mà BM=CM
nên HI=IK
=>I là trung điểm của HK
7 tháng 2 2023
#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`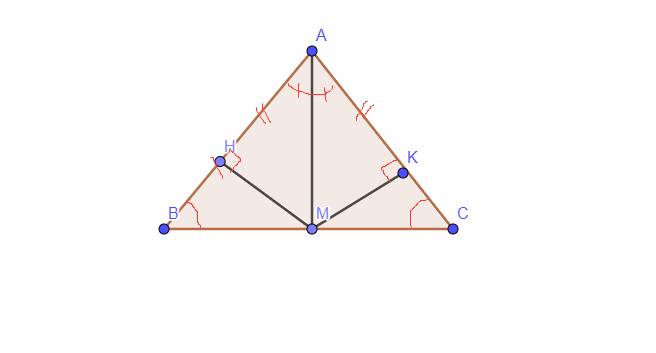
12 tháng 7 2023
Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
=>ΔABM=ΔACM
=>MB=MC
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
góc HAM=góc KAM
=>ΔAHM=ΔAKM
=>AH=AK
Xét ΔABC có AH/AB=AK/AC
nên HK//BC
Mik làm lại hình
a, Xét tam giác ABM và tam giác ACM có
BM=CM(Vì M là trung điểm của BC)
AB=AC(GT)
Am là cạnh chung
=> Tam giác ABM=Tam giác ACM (c.c.c)
=> Góc AMB=Góc AMC(2 góc tương ứng)
Mà góc AMB+góc AMC=\(180^o\)
=> Góc AMB=góc AMC=\(90^o\)
Vậy AM vuông góc BC
b, Xét tam giác AHM và tam giác AKM có:
Góc H=Góc K\(\left(=90^o\right)\)
AM là cạnh chung
Góc A là góc chung
=> Tam giác AHM=Tam giác AKM (cạnh huyền-góc nhọn)
=> AH=AK(2 cạnh tương ứng)
c, Mik chịu...