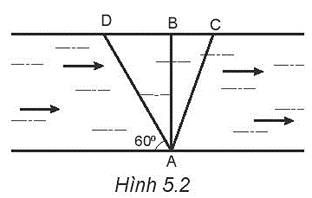
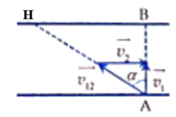
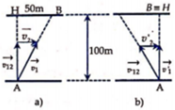
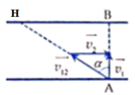
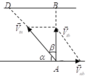
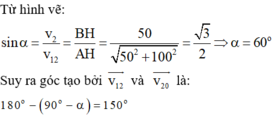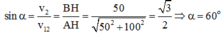Hai điểm A, B nằm trên cùng một bờ sông, điểm C nằm trên bờ đối diện sao cho đoạn AC vuông góc với dòng chảy. Các đoạn AB và AC bằng nhau. Một lần, người đánh cá từ A hướng mũi thuyền đến C1 để thuyền cập bến ở C rồi bơi ngay về A theo cách đó thì mất t1 giờ. Lần sau, ông hướng mũi thuyền sang C thì bị trôi xuống điểm C2 (C nằm giữa C1 và C2), phải bơi ngược lên C, sau đó bơi ngay về A theo cách đó thì mất t2 giờ. Lần thứ ba, ông bơi xuống B rồi về A thì mất t3 giờ.
a) Hỏi lần bơi nào mất ít thời gian nhất ? Lần bơi nào mất nhiều thời gian nhất ?
b) Xác định tỉ số giữa vận tốc vn của dòng nước và vận tốc v của thuyền, biết rằng tỉ số giữa t1 và t3 là 4/5.
Xem vận tốc thuyền do mái chèo và vận tốc dòng chảy mọi lần là như nhau.
ĐA: t1 < t3 < t2; 3/5