Cho tam giác ABC, đường thẳng song song với BC cắt AB; AC theo thứ tự tai D và E. Vẽ đường thẳng a qua A vad song song BC, đường thẳng a cắt đường thẳng BE và CD tai G và K. C/m: A là trung điểm của KG
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


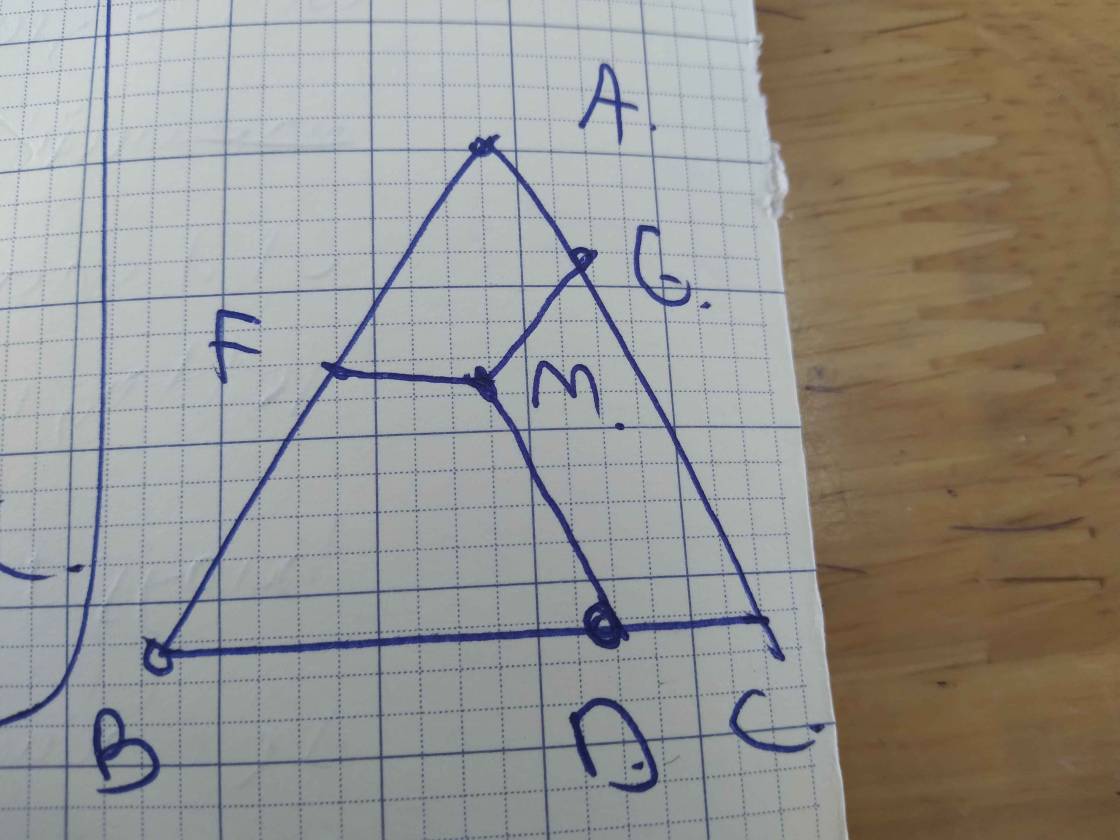
a: MD//AC
=>góc MDB=góc ACB
=>góc MDB=60 độ
Xét tứ giác BEMD có
EM//BD
góc B=góc MDB
=>BEMD là hình thang cân
ME//BC
=>góc AEM=góc ABD=60 độ
Xét tứ giác AEMF có
MF//AE
góc A=góc MEA
=>AEMF là hình thang cân
MF//AE
=>góc CFM=góc CAB=60 độ
Xét tứ giác DCFM có
DM//FC
góc DCF=góc MFC
=>DCFM là hình thang cân
b: Sửa đề: Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của tam giác nào
AEMF là hình thang cân
=>AM=EF
BEMD là hình thang cân
=>BM=ED
FMDC là hình thang cân
=>MC=FD
=>Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của ΔEFD

a: Xét ΔABC có DE//BC
nên AD/AB=DE/BC
=>DE/10=3/5
hay DE=6(cm)
b: Xét ΔADE và ΔCGE có
\(\widehat{ADE}=\widehat{CGE}\)
\(\widehat{AED}=\widehat{CEG}\)
Do đó: ΔADE\(\sim\)ΔCGE
Suy ra: AD/CG=AE/CE
hay \(AD\cdot CE=AE\cdot CG\)



DE // BC theo định lí ta lét trong\(\Delta ABC\) có
\(\dfrac{AD}{BD}=\dfrac{AE}{EC}\) (1)
AK // BC theo định lí ta lét trong \(\Delta DBC\) có
\(\dfrac{AK}{BC}=\dfrac{AD}{DB}\) (2)
AG // BC theo định lí ta lét trong \(\Delta BEC\) có
\(\dfrac{AG}{BC}=\dfrac{AE}{EC}\) (3)
từ (1) (2) (3) \(\Rightarrow\dfrac{AK}{BC}=\dfrac{AG}{BC}\)
\(\Rightarrow AK=AG\left(đpcm\right)\)