Hướng dẫn: 

Áp dụng định luật bảo toàn động lượng, chú ý rằng khi lên đến điểm cao nhất vận tốc của lựu đạn nằm theo phương ngang, ta thu được các kết quả sau:

a) Vận tốc mảnh thứ hai có độ lơn $40m/s$ và có phương lệch $30^{0}$ so với phương ngang.

b) Mảnh thứ hai lên đến độ cao cực đại là $h=25m$.

mình chỉ cần hình thôi mong bạn vẽ hình vào chút

Áp dụng định lý sin: \(\dfrac{p}{sin90^0}=\dfrac{p_2}{sin30^0}\) (\(p_1\perp p_2\))

\(\Leftrightarrow\dfrac{mv}{sin90^0}=\dfrac{\dfrac{mv_2}{2}}{sin30^0}\)

\(\Leftrightarrow v_2=300\left(\dfrac{m}{s}\right)\)

Chọn A

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.

Theo định luật bảo toàn động lượng  p → = p → 1 + p → 2

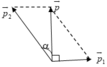
Với  p = m v = 2.250 = 500 ( k g m / s ) p 1 = m 1 v 1 = 1.500 = 500 ( k g m / s ) p 2 = m 2 v 2 = v 2 ( k g m / s )

Vì

  v → 1 ⊥ v → ⇒ p → 1 ⊥ p →   t h e o   p i t a g o   ⇒ p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 ( k g m / s )

⇒ v 2 = p 2 = 500 2 ( m / s ) M à   sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0

Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc  45 0  với vận tốc  500 2 ( m / s )

em chưa hoc 

hình hơi xấu(hình vẽ bằng tay) mong bạn thông cảm

chọn gốc tọa độ tại mặt đất, trục Ox nằm ngang cùng chiều chuyển động của đạn, trục Oy hương lên thẳng đứng

a) tại điểm cao nhất vân tốc của vật theo phương ngang

\(v_x=v_0.cos\alpha\)=\(5\sqrt{3}\)m/s

độ cao cực đại vật đạt được

\(H=\dfrac{v_0^2.sin\alpha^2}{2g}\)=1,25m

nổ thành hai mảnh bằng nhau

\(\dfrac{m}{2}=m_1=m_2\)

\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)

từ hình \(\Rightarrow\)\(p_2^2=\sqrt{p^2+p_1^2}\)

\(\left(m_2.v_2\right)^2=\left(m.v\right)^2+\left(m_1.v_1\right)^2\) (m₁=m₂)

\(\left(\dfrac{m}{2}.v_2\right)^2=m^2.v^2+\dfrac{m^2}{4}.v_1\)

\(\Rightarrow v_2=\)20m/s

theo hình ta có

\(tan\alpha=\dfrac{p_1}{p}\Rightarrow\alpha\)=60⁰

c)độ cao cực đại viên đạn thứ hai đạt được so với điểm ném

\(H'=\dfrac{v_2^2.sin^260^0}{2g}+H\)=16,25m

em không biết vẽ parabol thầy ạĐặng Trung Đức