Cho tam giác ABC. Vẽ cung tròn tâm C bán kính bằng AB, cung tròn tâm B bán kính bằng AC, hai cung tròn này cắt nhau tại D (A, D thuộc hai nữa mặt phẳng đối nhau bờ BC) . Chứng minh rằng:
a) △ABC = △DBC
b) CD // AB, BD // AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
ΔΔABC và ΔΔDCB có AB=CD (gt)
BC chung AC=DB (gt)
Vậy ΔΔABC = ΔΔDCB (c.c.c)
Suy ra ˆBDC=ˆA=800BDC^=A^=800 (hai góc tương ứng)
b) Do ΔΔABC = ΔΔDCB (câu a) do đó ˆABC=ˆBCDABC^=BCD^ (hai góc tương ứng của hai tam giác bằng nhau)
Hai góc này ở vị trí so le trong của hai đường thẳng AB và CD cắt đường thẳng BC do đó CD // AB.

Mong các bạn giải nhanh giúp mình. Mai mình phải đi học rùi!!!!![]()

Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
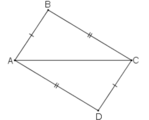
a: Xét ΔABC và ΔDBC có
AB=DB
AC=DC
BC chung
Do đó: ΔABC=ΔDBC
b: Xét tứ giác ABDC có
AB=CD
AC=BD
Do đó; ABDC là hình bình hành
Suy ra: CD//AB và BD//AC