chả biết

Gỉa sử : A,B,C thẳng hàng

=>AB+BC=AC

Hay 3+4=5(vô lí)

=> A,B,C ko thẳng hàng

THAM KHẢO:

Vì AB và AC cùng vuông góc với một mặt phẳng (P) nên AB trùng AC

 A, B, C thẳng hàng.

REFER

a) Do C nằm giữa A và B

Mà : AB=4cm ;AC=1cm

⇒ AB=CB+AC

⇒ 4=CB+1

⇒ CB=4-1=3cm

Vậy : CB=3cm

b)  ta có BD=2cm ; CB=3cm

⇒ CD=BD+CB

⇒ CB=2+3=5cm

Vậy : CB=5cm

TK

ABCD

a) Do C nằm giữa A và B

Mà : AB=4cm ;AC=1cm

 AB=CB+AC

 4=CB+1

 CB=4-1=3cm

Vậy : CB=3cm

b) Như hình vẽ ta thấy BD=2cm ; CB=3cm

 CD=BD+CB

 CB=2+3=5cm

Vậy : CB=5cm

b,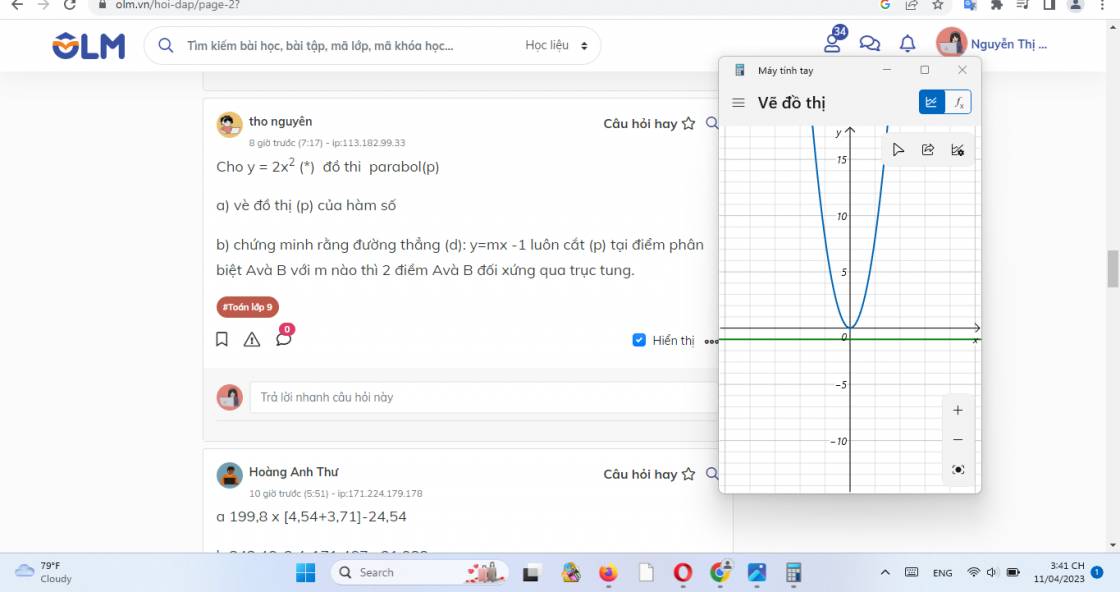 

Giả sử m = 0 thì đt có dạng y = -1

Quan sát hai đồ htij trên hình vẽ em sẽ thấy

parapol (p) và đt d không cắt nhau vậy việc chứng minh (p) và (d) cắt nhau tại hai điểm phân biệt với mọi m là không thể xảy ra 

giúp mk với

Vì 3 điểm A,B,C thằng hàng
mà AB = 5cm> BC = 2cm
\(\Rightarrow\)C là điểm nằm giữa A và B
Do đó : AC + BC = AB

\(\Leftrightarrow\)AC           = AB - BC = 5 - 2 = 3(cm )
Vậy AC = 3cm

AC = 3 cm nha bạn

k tui nha

thanks

a) Bạn ghi câu a) không rõ ràng nên mình thay thế bằng ý kiến của mình nhé !

CMR : \(\Delta ABE=\Delta HBE\)

Xét \(\Delta ABE,\Delta HBE\) có :

\(BA=BH\left(gt\right)\)

\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác của \(\widehat{B}\) )

\(BE:chung\)

=> \(\Delta ABE=\Delta HBE\left(c.g.c\right)\)

b) Gọi \(AH\cap BE=\left\{O\right\};O\in BE\)

Xét \(\Delta ABO,\Delta HBO\) có :

\(AB=BH\left(gt\right)\)

\(\widehat{ABO}=\widehat{HBO}\) (BE là tia phân giác của \(\widehat{B}\) ; \(O\in BE\))

AO : Chung

=> \(\Delta ABO=\Delta HBO\left(c.g.c\right)\)

=> \(\widehat{BOA}=\widehat{BOH}\) (2 góc tương ứng)

Mà : \(\widehat{BOA}+\widehat{BOH}=180^o\left(Kềbù\right)\)

=> \(\widehat{BOA}=\widehat{BOH}=\dfrac{180^o}{2}=90^o\)

=> \(BO\perp AH\)

Hay : \(BE\perp AH\)

c) Ta chứng minh được : \(\Delta BKE=\Delta BCE\)

Suy ra : \(EK=EC\) (2 cạnh tương ứng)

d) Xét \(\Delta ABC\) có :

BE là tia phân giác của \(\widehat{ABC}\) (1)

Xét \(\Delta KEM,\Delta CEM\) có :

\(EK=EC\left(cmt\right)\)

\(EM:chung\)

\(KM=CM\) (M là trung điểm của KC)

=> \(\Delta KEM=\Delta CEM\left(c.c.c\right)\)

=> \(\widehat{MEK}=\widehat{MEC}\) (2 góc tương ứng)

=> EM là tia phân giác của \(\widehat{KEC}\) (2)

Từ (1) và (2) => \(BE\equiv ME\)

=> B, E, M thẳng hàng

=> đpcm.

góc BKE và góc BCE bằng nhau theo trường hợp gì vậy bạn