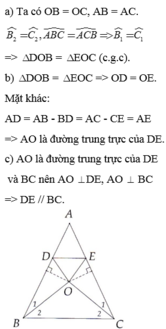
cho tam giác abc .các đường trung tuyến bd và ce cắt nau tại g, qua điểm o thuộc cạnh bc vẽ om//bd (m thuộc ab;n thuộc ac).m,n cắt bd và ce thứ tự ở i,k

   a, gọi h là giao điểm của om,bd. tính tỉ số 

   b, chứng minh mi=\(\frac{1}{3}\)mn

   c, vhuwngs minh mi=ik=kn

Cho tam giác ABC nhọn. Vẽ đường cao BD và CE của tam giác, biết D thuộc cạnh AC, E thuộc cạnh AB. CE và BD cắt nhau tại H. Gọi I, K lần lượt là trung điểm của BC và AH. Chứng minh rằng: a) Bốn điểm B, C, E, D cùng thuộc đường tròn tâm I. I. b) Tứ giác IEKD nội tiếp được trong một đường tròn.

cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau tại O. Gọi M là điểm bất kỳ trên cạnh BC. Vẽ MG song song với BD ( G thuộc AC), vẽ MH song song với CE (E thuộc AB). Chứng minh rằng:

a) HI=IF=FG

b) OM đi qua trung diểm của HG

Cho tam giác ABC, trung tuyến BD, CE. Gọi M là 1 điểm bất kì thuộc BC. Qua M vẽ đường thẳng song song với AC, AB lần lượt cắt BD, CE tại K và H. CMR: BD và CE chia KH thành 5 đoạn bằng nhau.

Bài 1: Cho tam giác ABC có đường truyến BD và CE cắt nhau tại G. Gọi I, K là trung điểm GB, GC. Chứng minh DE// IK và DE = IK.

Bài 2: Cho tam giác ABC có đường trung tuyến BD và CE. Gọi M, N là trung điểm BE, CD. Gọi MN cắt BD tại I và MN cắt CE tại I. Chứng minh MI = IK = KN.

1: Cho tam giác ABC cân tại A. Điểm D thuộc cạnh BC, điểm E thuộc tia đối của tia CB sao cho BD=CE. Các đường vuông góc với BC từ D và E cắt AB và AC ở M,N. CMR

a) MD=EN

b) BC cắt MN tại trung điểm I ở MN

Cho tam giác ABC cân tại A. Các đường trung trực của AB và AC cắt nhau tại O. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho BD = CE. Chứng minh:

a)  ∆ D O B   =   ∆ E O C ;

b) AO là đường trung trực của DE;

c) DE // BC.