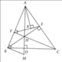
CHo tam giác ABC có 3 góc nhọn và các đường cao AD, BE và CF cắt nhau tại H.
a. Chứng minh rằng ΔAEF ∼ Δ ABC và ΔAEF ∼ ΔDBF
b. CHứng minh rằng \(\dfrac{AF}{FB}.\dfrac{BD}{DC}.\dfrac{CE}{EA}=1\)
c. Giả sử SAEF= SBDF=SCED. CHứng minh rằng ΔABC và ΔDEF đồng dạng rồi suy ra ΔDEF đều