Bài 1: Cho tam giác ABC vuông tại A. Biết AB = 8cm, AC = 6cm
a. Tính BC
b. Vẽ ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác ABC. Tính BN và CP
c. Tính GN và GC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 7 2015
a) Áp dụng định lí Py-ta-go vào tam giác ACM, ta có:
\(AM^2+CM^2=CA^2\)
Hay \(3,5^2+CM^2=5^2\)=>\(CM^2\)=25-12,25=12,75 => CM=\(\sqrt{12,75}\)
Vì M là trung điểm của CB => CM =MB =\(\sqrt{12,75}\)
=> CB= 2. \(\sqrt{12,75}\) =\(\sqrt{51}\)
Áp dụng định lí Py-ta-go vào tam giác ABC, ta có:
AC^2+AB^2=BC^2
Hay 5^2+AB^2=\(\sqrt{51}^2\)
=>AB=\(\sqrt{26}\)
b) BN=\(\frac{\sqrt{26}}{2}\)
CP=\(\frac{\sqrt{74}}{2}\)
Hình như vậy đó bạn
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
24 tháng 4 2019
a)tam giác abc vuông tại a nên theo định lí Py-ta-go,ta có :
BC2 =AC2+AB2
hay BC^2 =12^2+9^2
BC^2=81+144=225
BC=15CM
b) tam giác abc vuông tại a có đường trung tuyến ứng với cạnh huyền bc
=> AM=1/2 BC
hay AM=1/2.15
AM=7.5 cm
ta có g là trọng tâm cura tam giác abc
=> GM=1/3 AM ( tính chất đường trung tuyến )
GM=1/3.7,5
GM=2,5 cm
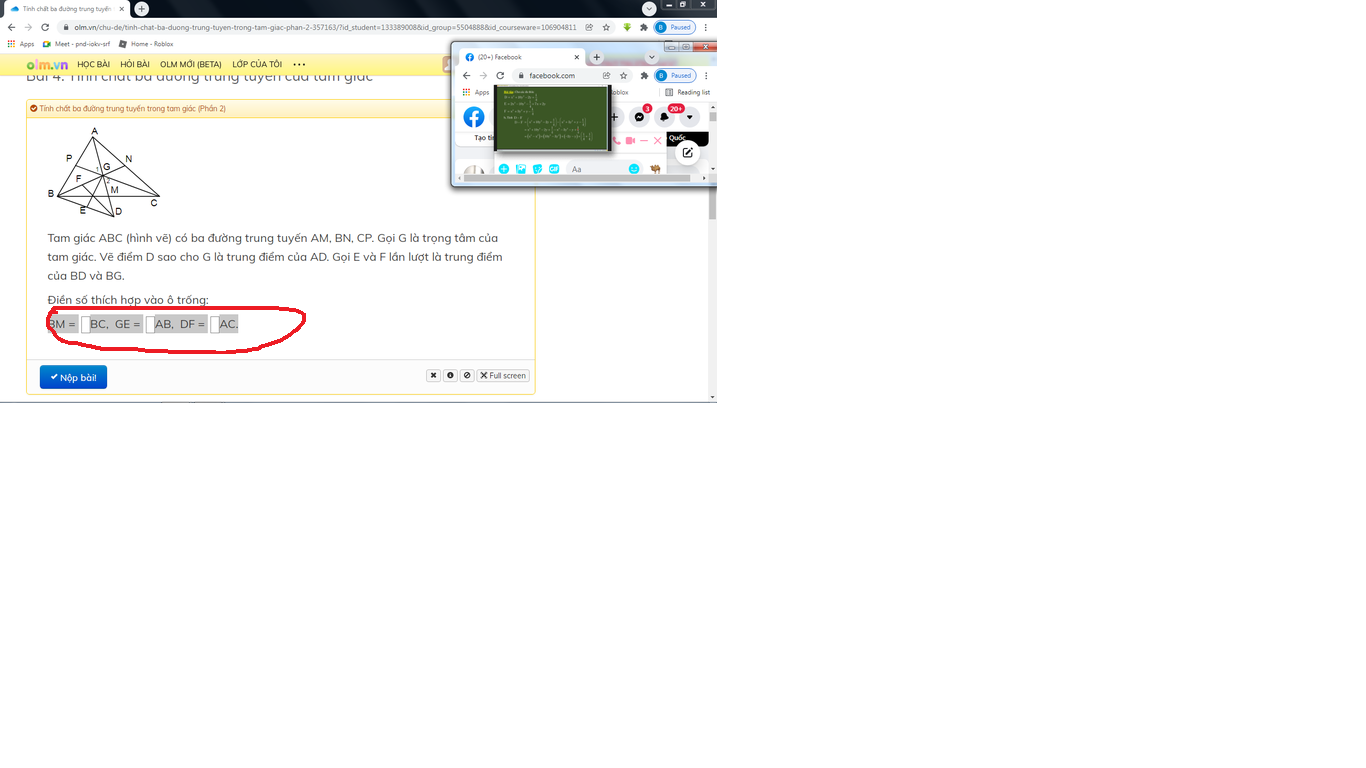
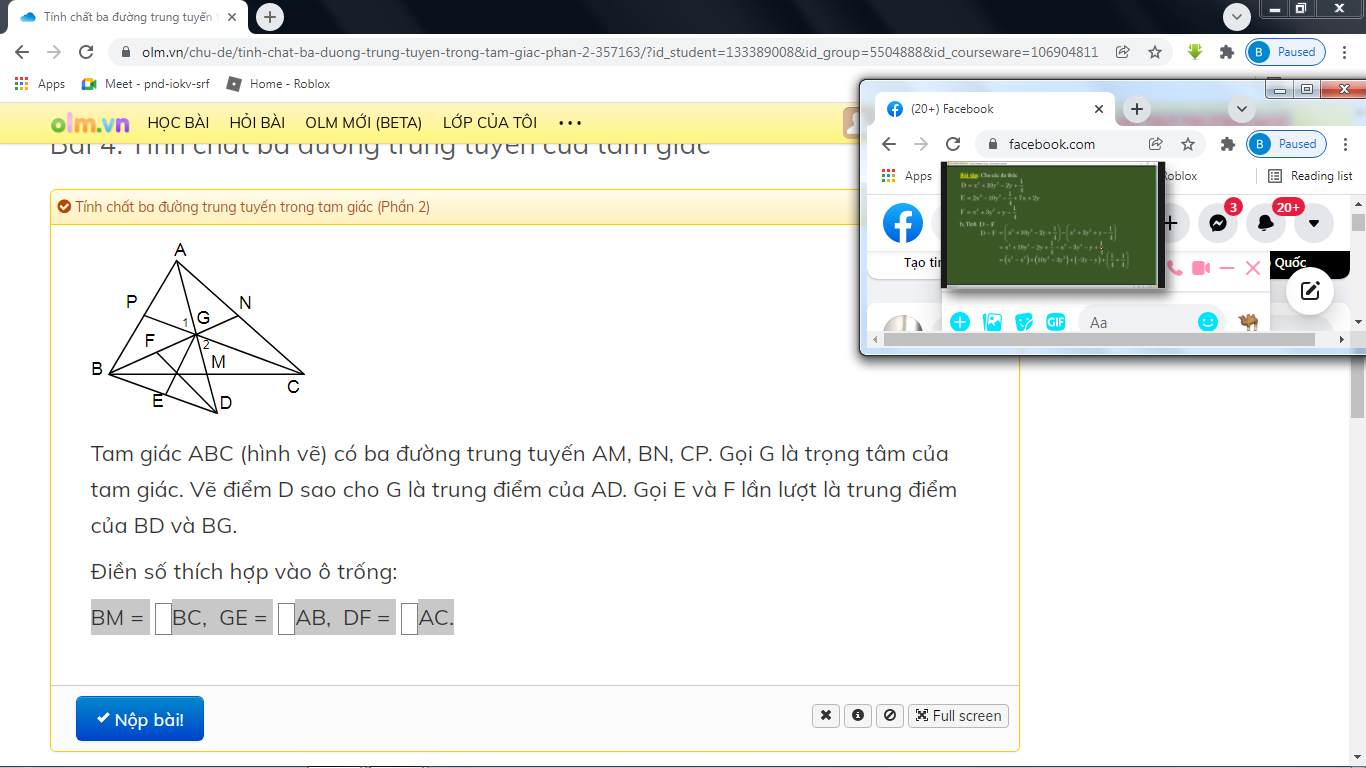
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)