Tham khảo:

a) Ta có: \(\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {MA}  + \left( {\overrightarrow {MA}  + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA}  + \overrightarrow {AC} } \right) = \overrightarrow 0 \)

\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MA}  + \overrightarrow {AB}  + 2\overrightarrow {AC}  = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {AM}  = \overrightarrow {AB}  + 2\overrightarrow {AC} \\ \Leftrightarrow \overrightarrow {AM}  = \frac{1}{4}\overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AC} \end{array}\)

Trên cạnh AB, AC lấy điểm D, E sao cho \(AD = \frac{1}{4}AB;\;\,AE = \frac{1}{2}AC\)

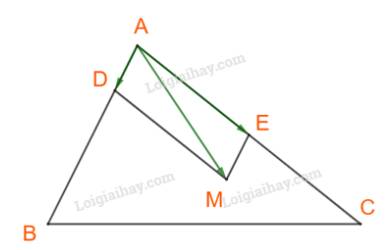
Khi đó \(\overrightarrow {AM}  = \overrightarrow {AD}  + \overrightarrow {AE} \) hay M là đỉnh thứ tư của hình bình hành AEMD.

b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  = 4\overrightarrow {OM} \)

Với mọi điểm O, ta có: \(\left\{ \begin{array}{l}\overrightarrow {OA}  = \overrightarrow {OM}  + \overrightarrow {MA} ;\;\\\overrightarrow {OB}  = \overrightarrow {OM}  + \overrightarrow {MB} ;\;\,\\\overrightarrow {OC}  = \overrightarrow {OM}  + \overrightarrow {MC} \end{array} \right.\)

\(\begin{array}{l} \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  = \left( {\overrightarrow {OM}  + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM}  + \overrightarrow {MB} } \right) + 2\left( {\overrightarrow {OM}  + \overrightarrow {MC} } \right)\\ = 4\overrightarrow {OM}  + \left( {\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC} } \right) = 4\overrightarrow {OM}  + \overrightarrow 0  = 4\overrightarrow {OM} .\end{array}\)

Vậy với mọi điểm O, ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  = 4\overrightarrow {OM} \).

Tham khảo cách 2 câu a: 

Cách 2:

Ta có: \(\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0  \Leftrightarrow \left( {\overrightarrow {MC}  + \overrightarrow {CA} } \right) + \left( {\overrightarrow {MC}  + \overrightarrow {CB} } \right) + 2\overrightarrow {MC}  = \overrightarrow 0 \)

\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MC}  + \overrightarrow {CA}  + \overrightarrow {CB}  = \overrightarrow 0 \\ \Leftrightarrow 4.\overrightarrow {CM}  = \overrightarrow {CA}  + \overrightarrow {CB} \end{array}\)

Gọi D là đỉnh thứ tư của hình bình hành ACBD.

Khi đó: \(\overrightarrow {CD}  = \overrightarrow {CA}  + \overrightarrow {CB} \)\( \Rightarrow 4.\overrightarrow {CM}  = \overrightarrow {CD} \)

\( \Leftrightarrow \overrightarrow {CM}  = \frac{1}{4}\overrightarrow {CD}  \Leftrightarrow \overrightarrow {CM}  = \frac{1}{2}\overrightarrow {CO} \)

Với O là tâm hình bình hành ACBD, cũng là trung điểm đoạn AB.

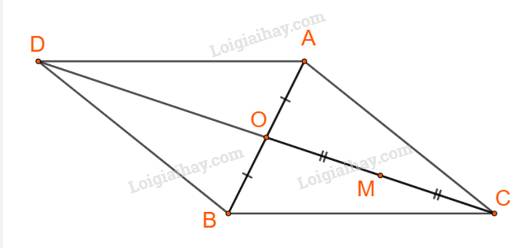
Vậy M là trung điểm của trung tuyến kẻ từ C của tam giác ABC.

a) \(\overrightarrow {OA}  + 3\overrightarrow {OB}  = \overrightarrow 0 \)

\(\begin{array}{l}
\overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\
\Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\
\Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB}
\end{array}\)

Vậy O thuộc đoạn AB sao cho \(OB = \frac{1}{4}AB\)

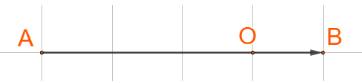
b) Ta có: 

\(\begin{array}{l}
\overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\
= \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\
= 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm)
\end{array}\)

1.

\(\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{AI}=\overrightarrow{0}\Leftrightarrow\overrightarrow{IB}+\overrightarrow{AC}=0\)

\(\Leftrightarrow\overrightarrow{IB}=\overrightarrow{CA}\)

\(\Rightarrow\) I là 1 đỉnh của hình bình hành ABIC

2.

Gọi N là trung điểm AB \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AB}\)

\(\overrightarrow{MA}+\overrightarrow{BM}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BA}+2\overrightarrow{MC}=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{MC}=\dfrac{1}{2}\overrightarrow{AB}\Leftrightarrow\overrightarrow{MC}=\overrightarrow{AN}\)

\(\Rightarrow\) M là 1 đỉnh của hình bình hành ANCM

Gọi G là trọng tâm của \(\Delta\)ABC. Khi đó, với mỗi điểm O ta luôn có:

\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}\). Suy ra \(3\overrightarrow{OG}=2\overrightarrow{CB}\)

Do G xác định nên ta có thể dựng điểm O sao cho: OG = 2/3.BC và \(\overrightarrow{OG}\uparrow\uparrow\overrightarrow{CB}\)như hình vẽ:

Copy làm j cho tốn công, ko đc tick đâu!!!

a) Giả sử điểm I thỏa mãn:
\(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{0}\)\(\Leftrightarrow\overrightarrow{IA}-\overrightarrow{IC}+\overrightarrow{IB}-\overrightarrow{IC}+2\overrightarrow{IB}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{CA}+\overrightarrow{CB}+2\overrightarrow{IB}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{IB}=\overrightarrow{AC}+\overrightarrow{BC}\)
\(\Leftrightarrow\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\).
Xác định véc tơ: \(\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\).

Dựng điểm B' sao cho \(\overrightarrow{BC}=\overrightarrow{CB'}\).
\(\overrightarrow{AC}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB'}=\overrightarrow{AB'}\).
\(\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}=\dfrac{\overrightarrow{AB'}}{2}\).
Dựng điểm I sao cho \(\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}=\overrightarrow{AK}\) (K là trung điểm của AB').

b) Tìm điểm I sao cho: \(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{0}\) và chứng mịn điểm I cố định.
Có: \(\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{IA}+3\overrightarrow{IB}+2\overrightarrow{CI}\)
\(=\left(\overrightarrow{CI}+\overrightarrow{IA}\right)+\left(\overrightarrow{CI}+\overrightarrow{IB}\right)+2\overrightarrow{IB}\)
\(=\overrightarrow{CA}+\overrightarrow{CB}+2\overrightarrow{IB}\).
Suy ra: \(\overrightarrow{CA}+\overrightarrow{CB}+2\overrightarrow{IB}=\overrightarrow{0}\)\(\Leftrightarrow\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\)
Vậy điểm I xác định sao cho \(\overrightarrow{IB}=\dfrac{\overrightarrow{AC}+\overrightarrow{BC}}{2}\) .
Do A, B, C cố định nên tồn tại một điểm I duy nhất.
Theo giả thiết:
Có \(\overrightarrow{MN}=\overrightarrow{MA}+3\overrightarrow{MB}-2\overrightarrow{MC}\)\(=\overrightarrow{MI}+\overrightarrow{IA}+3\left(\overrightarrow{MI}+\overrightarrow{IB}\right)-2\left(\overrightarrow{MI}+\overrightarrow{IC}\right)\)
\(=2\overrightarrow{MI}+\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}\)
\(=2\overrightarrow{MI}\) (Do các xác định điểm I).
Vì vậy \(\overrightarrow{MN}=2\overrightarrow{MI}\) nên hai véc tơ \(\overrightarrow{MN},\overrightarrow{MI}\) cùng hướng.
Suy ra 3 điểm M, N, I thẳng hàng hay MN luôn đi qua điểm cố định I.