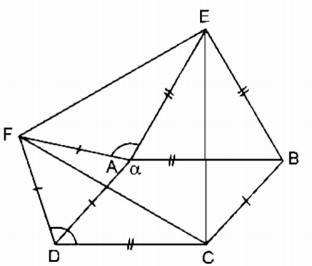
Cho hình bình hành ABCD có góc A=α>900. Ở phía ngoài hình bình hành, vẽ các tam giác đều ADF, ABE.
a. Tính góc EAF
b. Chứng minh rằng tam giác CEF là tam giác đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.

a) Tính góc EAF
EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1)
b) Chứng minh rằng tam giác CEF là tam giác đều
ABC^ = ADC^ = 180* - a
=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2)
CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3)
AF = DF = AD = BC (4)
CD = AB = BE = AE (5)
(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c)
=> CF = CE = EF => CEF là tam giác đều
a,tính góc EAF
EAF^=360* - ( DAF^+BAD^+BAE^)=360*-(60*+a+60*)=240*-a(1)
b,chứng minh rằng tam giác CÈ là tam giác đều
ABC^=ADC^+ADF^=180*-a+60*=240*-a(2)
CBE^=ABC^+ABE^=180*-a+60*=240*-a(3)
AF=DF=AD=BC(4)
CD=AB=BE=AE(5)
(1) (2) (3) (4) và (5) => tam giác CDF=tam giác EAF (c.g.c)
=> CF=CE=EF=>CÈ là tam giác đều

Tính góc EAF
EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1)
b) Chứng minh rằng tam giác CEF là tam giác đều
ABC^ = ADC^ = 180* - a
=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2)
CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3)
AF = DF = AD = BC (4)
CD = AB = BE = AE (5)
(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c)
=> CF = CE = EF => CEF là tam giác đều

Vì ∠ (BAD) + ∠ (BAE) + ∠ (EAF) + ∠ (FAD) = 360 0
⇒ ∠ (EAF) = 360 0 – ( ∠ (BAD) + ∠ (BAE) + ∠ (FAD) )
Mà ∠ (BAD) = α 2 (gt)
∠ (BAE) = 60 0 (ΔBAE đều)
∠ (FAD) = 60 0 (ΔFAD đều)
Nên ∠ (EAF) = 360 0 – ( α 2 + 60 0 + 60 0 ) = 240 0 – α

Bạn tự vẽ hình nhé!
Giải
a) Ta có:
\(\widehat{EAF}+\widehat{EAB}+\widehat{BAD}+\widehat{DAF}=360^0\)
\(\Rightarrow\widehat{EAF}+60^0+60^0+110^0=360^0\)
\(\Rightarrow\widehat{EAF}=130^o\)
b) Vì ABCD là hình bình hành nên:
\(\widehat{BAD}+\widehat{ADC}=180^o\)
\(110^o+\widehat{ADC}=180^o\)
\(\Rightarrow\widehat{ADC}=70^o\)
\(\Rightarrow\widehat{CDF}=\widehat{ADC}+\widehat{ADF}=70^o+60^o=130^o\)
Xét \(\Delta\)EAF và \(\Delta\)CDF có:\(\hept{\begin{cases}AE=DC\left(=AB\right)\\AF=DF\\\widehat{EAF}=\widehat{CDF}=130^o\end{cases}\Rightarrow\Delta EAF=\Delta CDF\left(cgc\right)}\)
c) Ta có: \(\Delta EAF=\Delta CDF\left(cmt\right)\Rightarrow EF=CF\)
Tương tự cũng có: \(\Delta CDF=\Delta EBC\left(cgc\right)\Rightarrow CF=EC\)
\(\Rightarrow\Delta\)EFC là tam giác đều (đpcm)