Cho 2 hình vuông ABCD và AEFG có chung đỉnh A và 2 đỉnh B;E nằm trong 1 mặt phẳng bờ CF. Gọi N;Q lần lượt là tâm của 2 hình vuông trên. Lấy M và P là trung điểm của BE và DG. Chứng minh MNPQ là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



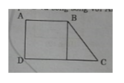
a) Đáy lớn của hình thang ABCD là : 16 x 2 = 32 ( cm )
Diện tích hình thang ABCD đó là : ( 32 + 16 ) x10 : 2 = 240 ( cm2)
b) Độ dài đoạn thẳng AM ( hay chính là đoạn thẳng MD ) là : 10 : 2 = 5 ( cm )
Diện tích hình tam giác ABM là : 16 x 5 : 2 = 40 ( cm2 )
Diện tích hình tam giác MDC là : 32 x 5 :2 = 80 ( cm2 )
Diện tích hình tam giác MBC là : 240 - ( 80 + 40 ) = 120 (cm2)
Đáp số : 120 cm2
Vậy diện tích hình tam giác MBC là 120 cm2

Gọi I là tâm của hình vuông thì I chính là hình chiếu của C lên BD
Ta có: I ( -1+4t;1-t;-1+t )nên C I → = 4 t - 2 ; 2 - t ; t + 1
Vì C I ⊥ B D nên
C I ⇀ . u B D → = 0 ⇔ 4 4 t - 2 - 2 - t + t + 1 = 0 ⇔ t = 1 2
Do đó: I 1 ; 1 2 ; - 1 2 , C I - 3 2 2
I là trung điểm AC ⇒ A ( 1;2;3 )
Tọa độ điểm B - 1 + 4 t ; 1 - t ; - 1 + t với t > 1 4
Ta có IB = IC nên
- 2 + 4 t 2 + 1 2 - t 2 + 1 2 + t 2 = 9 2 ⇔ t 2 - t = 0 ⇔ t = 0 t = 1
Tọa độ điểm B ( 3;0;0 ). Suy ra d ( -1;1;-1 )
Đáp án D

Chọn A
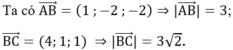
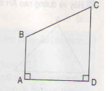
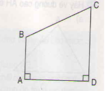
Theo giả thiết ABCD vuông tại A và B và có diện tích bằng 6√2 nên:
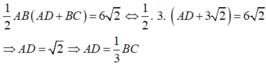
Do ABCD là hình thang vuông tại A và B nên ![]() . Giả sử khi đó ta có:
. Giả sử khi đó ta có:


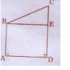
- Học sinh dùng ê – ke vẽ như hình dưới
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật

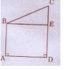
- Học sinh dùng ê – ke vẽ như hình dưới
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật

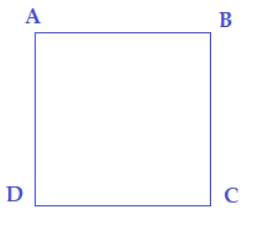
Vì ABCD là hình vuông nên AB = BC = CD = DA ( tính chất)
a) Ta có: +) BA = BC nên đỉnh B cách đều hai điểm A và C
+) DA = DC nên đỉnh D cách đều hai điểm A và C
Vậy đỉnh B và D cách đều hai điểm A và C
b) +) Vì CB = CD nên khoảng cách từ C đến 2 đường thẳng AB và AD bằng nhau. Do đó đỉnh C cách đều 2 đường thẳng AB và AD.
+) Khoảng cách từ A đến AB bằng khoảng cách từ A đến AD ( bằng 0) nên A cách đều hai đường thẳng AB và AD.
Vậy đỉnh C và đỉnh A cách đều hai đường thẳng AB và AD.