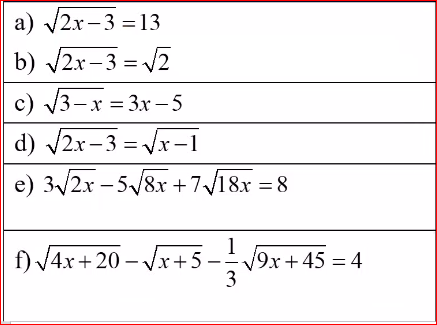
giúp em câu e và f ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(k,=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)+5\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}+5}\\ =\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}+5\right)}{\sqrt{a}+\sqrt{b}+5}=\sqrt{a}-\sqrt{b}\)
\(h,=\dfrac{1}{2a-1}\sqrt{25a^2\left(a^2-4a+4\right)}=\dfrac{1}{2a-1}\sqrt{25a^2\left(a-2\right)^2}\\ =\dfrac{\left|5a\left(a-2\right)\right|}{2a-1}=\left[{}\begin{matrix}\dfrac{5a\left(a-2\right)}{2a-1}\left(a\ge2;a\ne\dfrac{1}{2}\right)\\\dfrac{5a\left(2-a\right)}{2a-1}\left(0\le a< 2;a\ne\dfrac{1}{2}\right)\\\dfrac{-5a\left(2-a\right)}{2a-1}\left(a< 0\right)\end{matrix}\right.\)

e) \(sin^22x-6sin2x+5=0\Rightarrow\) \(\left[{}\begin{matrix}sin2x=5\left(loại\right)\\sin2x=1\end{matrix}\right.\)
\(\Rightarrow sin2x=sin\left(\dfrac{\pi}{2}\right)\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k2\pi\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
f.
\(4cos^23x-2\left(\sqrt{3}+1\right)cos3x+\sqrt{3}=0\)
\(\Leftrightarrow4cos^23x-2cos3x-2\sqrt{3}cos3x+\sqrt{3}=0\)
\(\Leftrightarrow2cos3x\left(2cos3x-1\right)-\sqrt{3}\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left(2cos3x-\sqrt{3}\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\\cos3x=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)

e: vecto AM=(x-3;y+1)
vecto BM=(x+1;y-2)
vecto AC=(-2;0)
vecto AM=2*vecto BM-3*vecto AC
=>x-3=2*(x+1)+6 và y+1=2(y-2)
=>x-3=2x+8 và y+1=2y-4
=>x=-11 và y=5
f: Tọa độ H là:
\(\left\{{}\begin{matrix}x=\dfrac{3-1+1}{3}=1\\y=\dfrac{-1+2-1}{3}=0\end{matrix}\right.\)
g: K thuộc Oy nên K(0;y)
vecto AB=(-4;3)
vecto AK=(-3;y+1)
A,K,B thẳng hàng
=>\(-\dfrac{3}{-4}=\dfrac{y+1}{3}\)
=>y+1=9/4
=>y=5/4
h: P thuộc Ox nên P(x;0)
vecto PA=(x-3;1)
vecto PC=(x-1;1)
ΔPAC vuông tại P
=>vecto PA*vecto PC=0
=>(x-3)(x-1)+1=0
=>x^2-4x+3+1=0
=>x=2
=>P(2;0)

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)



e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
\(e,3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}=8\left(x\ge0\right)\\ \Leftrightarrow\sqrt{x}\left(3\sqrt{2}-5\sqrt{8}+7\sqrt{18}\right)=8\\ \Leftrightarrow\sqrt{x}\left(3\sqrt{2}-10\sqrt{2}+21\sqrt{2}\right)=8\\ \Leftrightarrow14\sqrt{2x}=8\Leftrightarrow\sqrt{2x}=\dfrac{4}{7}\Leftrightarrow2x=\dfrac{16}{49}\Leftrightarrow x=\dfrac{8}{49}\left(tm\right)\)
\(f,\sqrt{4x+20}-\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4\left(x\ge-5\right)\\ \Leftrightarrow2\sqrt{x+5}-\sqrt{x+5}-\dfrac{1}{3}\cdot3\sqrt{x+5}=4\\ \Leftrightarrow0\sqrt{x+5}=4\\ \Leftrightarrow\sqrt{x+5}=0\Leftrightarrow x+5=0\Leftrightarrow x=-5\left(tm\right)\)
e) \(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}=8\left(đk:x\ge0\right)\)
\(\Leftrightarrow3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}=8\)
\(\Leftrightarrow14\sqrt{2x}=8\Leftrightarrow\sqrt{2x}=\dfrac{8}{14}\Leftrightarrow2x=\dfrac{16}{49}\Leftrightarrow x=\dfrac{8}{49}\left(tm\right)\)
f) \(\sqrt{4x+20}-\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4\)
\(\Leftrightarrow2\sqrt{x+5}-\sqrt{x+5}-\sqrt{x+5}=4\)
\(\Leftrightarrow0=4\left(VLý\right)\)
Vậy \(x\in\left\{\varnothing\right\}\)