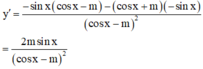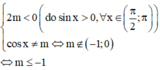Theo mình:

để hàm số đồng biến, đk cần là y'=0.

a>0 và \(\Delta'< 0\)

nghịch biến thì a<0 

vì denta<0 thì hầm số cùng dấu với a

mình giải được câu a với b

câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb) 

câu d dùng viet

câu e mình chưa chắc lắm ^^

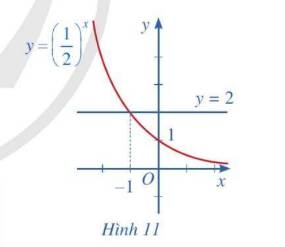
Do \(\dfrac{1}{2}< 1\) ⇒ Hàm số \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R.

\(\left(\dfrac{1}{2}\right)^x>2\\ \Rightarrow x< log_{\dfrac{1}{2}}2\\ \Rightarrow x< -1\)

Đáp án A

Để hàm số nghịch biến trên  π 2 ; π  ta cần có 

a) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).

Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\).

Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)

Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)

\({x_1},{x_2} \in \left( {0; + \infty } \right) \Rightarrow {x_1}{x_2} > 0\)

\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)

Vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).

b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).

Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)

Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)

\({x_1},{x_2} \in \left( { - \infty ;0} \right) \Rightarrow {x_1}{x_2} > 0\)(Cùng dấu âm nên tích cũng âm)

\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)

Vậy hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\).

a/

\(y=\frac{1}{sinx}+\frac{1}{cosx}\ge\frac{4}{sinx+cosx}=\frac{4}{\sqrt{2}sin\left(x+\frac{\pi}{4}\right)}\ge\frac{4}{\sqrt{2}}=2\sqrt{2}\)

\(y_{min}=2\sqrt{2}\) khi \(\left\{{}\begin{matrix}sinx=cosx\\sin\left(x+\frac{\pi}{4}\right)=1\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{4}\)

\(y_{max}\) không tồn tại (y dần tới dương vô cùng khi x gần tới 0 hoặc \(\frac{\pi}{2}\))

b/

\(y=\frac{1}{1-cosx}+\frac{1}{1+cosx}=\frac{1+cosx+1-cosx}{1-cos^2x}=\frac{2}{sin^2x}\)

Hàm số ko tồn tại cả min lẫn max ( \(0< y< \infty\))

c/

Do \(tan^2x\) ko tồn tại max (tiến tới vô cực) trên khoảng đã cho nên hàm ko tồn tại max

\(y=2+\frac{sin^4x+cos^4x}{\left(sinx.cosx\right)^2}+\frac{1}{sin^4x+cos^4x}\ge2+2\sqrt{\frac{sin^4x+cos^4x}{\frac{1}{4}sin^22x.\left(sin^4x+cos^4x\right)}}\)

\(y\ge2+\frac{4}{sin2x}\ge2+\frac{4}{1}=6\)

\(y_{min}=6\) khi \(\left\{{}\begin{matrix}sin2x=1\\sin^4x+cos^4x=sinx.cosx\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{4}\)