Gọi E và F lần lượt là trung điểm của AC và BD; E' và F' lần lượt là hình chiếu của E, F trên đường thẳng m.

Khi đó, GG' là đường trung bình của hình thang EE'F'F

⇒ G G ' = 1 2 EE' +FF').  

Mà EE' và FF' lần lượt là đường trung bình của hình thang AA'C'C và BB'D'D.

⇒ EE ' = 1 2 (AA' +CC') và FF ' = 1 2 (BB' +DD')  

Thay vào (1) ta được ĐPCM

đã hỏi thì hỏi ít thôi. hỏi lắm thế

hỏi 1 lần luôn cho lẹ, k cần mn giải hết đâu, biết bài nào thì giải giúp th

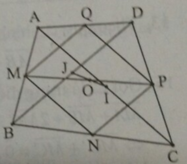
*Xét  tam giác ABC có M; N  là trung điểm của AB, BC nên MN là đường trung bình của tam giác.

⇒ M N / / A C ;     M N = 1 2 A C   ( 1 )

* Xét  tam giác ADC có P; Q  là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.

⇒ P Q / / A C ;     P Q = 1 2 A C   ( 2 )

* Từ (1) (2)  suy  ra  PQ// MN;  PQ = MN.  Do đó, tứ giác MNPQ là hình bình hành.

* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP

* Xét tam giác ABC có MI là đường trung bình nên:  M I / / B C ;    M I = 1 2 ​ B C   ( 3 )

* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên:  P J / / B C ;    P J = 1 2 ​ B C   ( 4 )

Từ (3) ( 4) suy ra ;  tứ giác  MIPJ là hình bình hành. Mà O là trung điểm MP nên  điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có  O I →   =   - O J →

Đáp án D

Chọn đáp án B

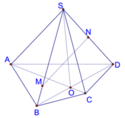
+ Giả sử SO, AD cắt nhau. Khi đó SO, AD đồng phẳng, suy ra S thuộc mp (ABCD) (Vô lý). Đáp án A bị loại.

+ Giả sử MN cắt SC. Khi đó MN và SC đồng phẳng, suy ra C thuộc (SBD) (Vô lý). Do đó đáp án C bị loại.

+ Giả sử SA cắt BC. Khi đó SA, BC đồng phẳng. Suy ra S thuộc mp (ABCD) (Vô lý). Đáp án D bị loại. MN, SO cùng nằm trong mp (SBD), không song song và trùng nhau.