Chứng minh công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều
S= V0t + \(\dfrac{1}{2}\)at2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Trong chuyển động thẳng nhanh dần đều thì vận tốc và gia tốc cùng dấu nhau a v 0 >0, quãng đường là đại lượng không âm.
⇒ phương án D – đúng.

CT quãng đường đi dc của chuyển động nhanh dần đều là:
\(s=v_0t+\dfrac{1}{2}at^2\)(a với v0 cùng dấu)

Đáp án B
Trong chuyển động thẳng chậm dần đều thì vận tốc và gia tốc ngược dấu nhau, quãng đường là đại lượng không âm

Đáp án A
Công thức tính quãng đường trong chuyển động nhanh dần đều là
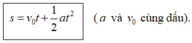

+ Công thức tính quãng đường trong chuyển động thẳng biến đổi đều:
v 0 t + 1 2 a t 2
+ Nếu chuyển động thẳng nhanh dần đều thì a và v 0 cùng dấu
+ Nếu chuyển động thẳng chậm dần đều thì a và v 0 trái dấu
=> Chọn A

Đáp án A
Công thức tính vận tốc trong chuyển động biến đổi đều: v = v0 + at.
Nếu chuyển động thẳng nhanh dần đều:
a cùng dấu với v0 (véc tơ gia tốc cùng phương
cùng chiều với véc tơ vận tốc).
Công thức tính quãng đường đi: s = v0t + at2

Công thức tính quãng đường đi :
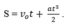
+ Chuyển động theo chiều (+) thì vo > 0.
+ Nhanh dần đều :a.v > 0 tức a cùng dấu với vo và v.
+ Chậm dần đều : a.v < 0 tức a trái dấu với vo và v.
Nhận xét : Quãng đường đi được trong các chuyển động thẳng biến đổi đều phụ thuộc vào thời gian theo hàm số bậc hai.

Chọn D.
Từ công thức v = vo + at
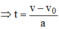
thế vào công thức:
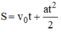
Ta được:
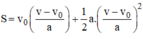
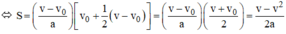
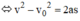
sách giáo khoa có đó bạn
trả lời các câu khác của tớ nx vứi