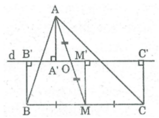
Cho tam giác ABC, trung tuyến AM. O là điểm thuộc AM. Qua O kẻ đường thẳng d cắt các cạnh AB, AC thứ tự ở D,E. Gọi A', B', C' là hình chiếu của A,B,C trên đường thẳng d. a) Nếu O là trung điểm AM.CMR AA'=(BB'+CC)/2. b) khi O là trọng tâm của tam giác ABC. Tìm mối liên hệ giữa AA', BB', CC'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2017
Ta có: BB’ ⊥ d (gt)
CC’ ⊥ d (gt)
Suy ra: BB’ // CC’
Tứ giác BB’CC’ là hình thang
Kẻ MM’ ⊥ d
⇒ MM’ // BB’ // CC’
Nên MM’ là đường trung bình của hình thang BB’CC’
⇒MM′=BB′+CC′2(1)⇒MM′=BB′+CC′2(1)
Xét hai tam giác vuông AA’O và MM’O:
ˆOA′A=ˆOM′MOA′A^=OM′M^
AO = MO (gt)
ˆAOA′=ˆMOM′AOA′^=MOM′^ (đối đỉnh)
Do đó: ∆ AA’O = ∆ MM’O (cạnh huyền, góc nhọn)
⇒ AA’ = MM’ (2)
Từ (1) và (2) suy ra: AA′=BB′+CC′2AA′=BB′+CC′/2.
CM
1 tháng 4 2019
Ta có: BB' ⊥ d (gt)
CC' ⊥ d (gt)
Suy ra: BB'// CC'
Tứ giác BB'C'C là hình thang
Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'
Lại có M là trung điểm của BC nên M' là trung điểm của B’C’
⇒ MM' là đường trung bình của hình thang BB'C'C
⇒ MM' = (BB' + CC') / 2 (1)
* Xét hai tam giác vuông AA'O và MM'O:
∠ (AA'O) = ∠ (MM' O) = 90 0
AO=MO (gt)
∠ (AOA') = ∠ (MOM' ) (2 góc đối đỉnh)
Do đó: ∆ AA'O = ∆ MM'O (cạnh huyền, cạnh góc nhọn)
⇒AA' = MM' (2)
Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2
3 tháng 9 2016
Từ M kẻ MH vuông góc với B'C' (H thuộc B'C')
Dễ dàng chứng minh được MH là đường trung bình của hình thang BCC'B'
=> \(MH=\frac{BB'+CC'}{2}\)
Dễ thấy tam giác OAA' = tam giác OHM (cạnh huyền - góc nhọn)
=> AA' = MH
=> \(BB'+CC'=2AA'\)
Bạn xem lại đề bài.