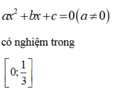Đáp án B

Đáp án B

\(a=-2b-5c\Rightarrow a+2b=-5c\)

- Với \(c=0\Rightarrow a=-2b\Rightarrow-\dfrac{b}{a}=\dfrac{1}{2}\)

\(ax^2+bx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{b}{a}=\dfrac{1}{2}\in\left(0;1\right)\end{matrix}\right.\) (thỏa mãn)

- Với \(c\ne0\)

Hàm \(f\left(x\right)=ax^2+bx+c\) liên tục trên R

\(f\left(0\right)=c\) ;

 \(f\left(\dfrac{1}{2}\right)=\dfrac{a}{4}+\dfrac{b}{2}+c=\dfrac{a+2b+4c}{4}=\dfrac{-5c+4c}{4}=-\dfrac{c}{4}\)

\(\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)=-\dfrac{c^2}{4}< 0;\forall c\)

\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) do \(\left(0;\dfrac{1}{2}\right)\subset\left(0;1\right)\)

Đề bài sai, ví dụ \(a=1;b=-\dfrac{5}{2};c=2\) thỏa mãn \(\dfrac{a}{6}+\dfrac{b}{5}+\dfrac{c}{6}=0\) nhưng phương trình \(x^2-\dfrac{5}{2}x+2=0\) vô nghiệm

\(Q=\dfrac{2-\dfrac{c}{a}-\dfrac{2b}{a}+\left(\dfrac{b}{a}\right)\left(\dfrac{c}{a}\right)}{1-\dfrac{b}{a}+\dfrac{c}{a}}=\dfrac{2-mn+2\left(m+n\right)-mn\left(m+n\right)}{1+m+n+mn}\)

\(Q=\dfrac{\left(2-mn\right)\left(m+n+1\right)}{\left(m+1\right)\left(n+1\right)}\ge\dfrac{\left[8-\left(m+n\right)^2\right]\left(m+n+1\right)}{\left(m+n+2\right)^2}\)

Đặt \(m+n=t\Rightarrow0\le t\le2\)

\(Q\ge\dfrac{\left(8-t^2\right)\left(t+1\right)}{\left(t+2\right)^2}-\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{\left(2-t\right)\left(4t^2+15t+10\right)}{4\left(t+2\right)^2}+\dfrac{3}{4}\ge\dfrac{3}{4}\)

Dấu "=" xảy ra khi \(t=2\) hay \(m=n=1\)

Thầy ơi sao bên này là (2-mn) qua bên kia lại là \(\left[8-\left(m+n\right)^2\right]\) , dưới mẫu là (m+1)(n+1) qua bên này là \(\text{(m+n+2)}^2\)

Với các số thực dương a, b, c ta có:

\(\frac{2b-c}{a}\ge4\Leftrightarrow2b-c\ge4a\Leftrightarrow b\ge\frac{4a+c}{2}\)

\(\Leftrightarrow b^2\ge\frac{16a^2+8ac+c^2}{4}\Leftrightarrow b^2-4ac\ge\frac{16a^2+c^2}{4}>0\)

=> phương trình \(ãx^2+bx+c=0\) luôn có nghiệm

+) Nếu \(ac\le0\Rightarrow\)Phương trình có nghiệm

+) Nếu ac > 0\(\Rightarrow\)a và c cùng dấu

Từ giả thiết suy ra \(\frac{2b}{a}\ge\frac{c}{a}+4>0\Rightarrow\)a và b cùng dấu

\(\Rightarrow\)a, b, c cùng dấu. Vì thế ta chỉ cần xét a, b và c cùng dương là đủ

Với a, b, c cùng dương ta có :

\(\frac{2b}{a}\ge\frac{c}{a}+4\Leftrightarrow b\ge\frac{c+4a}{2}\Leftrightarrow b^2\ge\frac{c^2+8ac+16a^2}{4}\)

\(\Leftrightarrow b^2-4ac\ge\frac{c^2-8ac+16a^2}{4}=\frac{\left(c-4a\right)^2}{4}\ge0\)

\(\Delta\ge0\)nên phương trình luôn có nghiệm

Vậy phương trình \(ax^2+bx+c=0\)luôn có nghiệm (đpcm)

Đặt \(f\left(x\right)=ax^2+bx+c\).

\(f\left(0\right)=c;f\left(1\right)=a+b+c\)

Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).