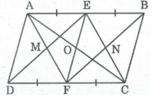
Cho hình bình hành ABCD. Gọi E,F theo thứ tự là trung điểm của AB,CD.
a) Chứng minh: AF song song CE.
b) Gọi M,N theo thứ tự là giao điểm của BD với AF,CE.
Chứng minh: Dm=MN=NB.
c) Chứng minh: AC,BD và EF đồng qui
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2021
a) Ta có: AB=CD(ABCD là hình bình hành)
mà \(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
và \(DF=FC=\dfrac{DC}{2}\)(F là trung điểm của DC)
nên AE=EB=DF=FC
Xét tứ giác AECF có
AE//CF(ABCD là hình bình hành)
AE=CF(cmt)
Do đó: AECF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
14 tháng 7 2021
b) Xét ΔABM có
E là trung điểm của AB(gt)
EN//AM(cmt)
Do đó: N là trung điểm của BM(Định lí 1 về đường trung bình của tam giác)
Suy ra: BN=NM(1)
Xét ΔDNC có
F là trung điểm của DC(gt)
FM//NC(cmt)
Do đó: M là trung điểm của DN(Định lí 1 về đường trung bình của tam giác)
Suy ra: DM=MN(2)
Từ (1) và (2) suy ra DM=MN=NB(Đpcm)
CC
11 tháng 12 2021
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
10 tháng 10 2021
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
9 tháng 10 2021
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
19 tháng 12 2021
a: Xét tứ giác EBFD có
EB//FD
EB=FD
Do đó: EBFD là hình bình hành
17 tháng 5 2022
Tham kHẢO 1; | - Vẽ hình đúng để làm được ý a
| 0,25
|
a) (1 điểm) - Chỉ ra được tứ giác DEBF là hình bình hành |
1.0 | |
b) (0,75 điểm). Gọi O là giao điểm của AC và BD - Chỉ ra trong hbh ABCD có O là trung điểm O của AC và BD (1) - Chỉ ra trong hbh có BD cắt EF tại trung điểm của mỗi đường. Mà O là trung điểm của BD nên O là trung điểm của EF (2) - Từ (1) và (2) ⇒ đpcm |
0.25
0.25 0.25 | |
c) (1 điểm) - Chỉ ra được M là trọng tâm của ΔABD ⇒ OM = - Chỉ ra được N là trọng tâm của ΔBCD ⇒ ON = - Mà OA = OC ⇒ OM = ON ⇒ đpcm |
![[Năm 2021] Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề)](https://vietjack.com/de-thi/images/de-thi-hoc-ki-1-toan-lop-8-co-dap-an-dtvj2021-71689.png)
![[Năm 2021] Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề)](https://vietjack.com/de-thi/images/de-thi-hoc-ki-1-toan-lop-8-co-dap-an-dtvj2021-71690.png)
OA![[Năm 2021] Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề)](https://vietjack.com/de-thi/images/de-thi-hoc-ki-1-toan-lop-8-co-dap-an-dtvj2021-71691.png)
OC
6 tháng 11 2021
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
CM
13 tháng 12 2017
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.