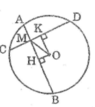
Ta có: HA = HB (gt)

Suy ra : OH ⊥ AB (đường kính dây cung)

Lại có : KC = KD (gt)

Suy ra : OK ⊥ CD (đường kính dây cung)

Mà AB > CD (gt)

Nên OK > OH (dây lớn hơn gần tâm hơn)

Áp dụng định lí Pitago vào tam giác vuông OHM ta có :

O M 2 = O H 2 + H M 2

Suy ra :  H M 2 = O M 2 - O H 2  (1)

Áp dụng định lí Pitago vào tam giác vuông OKM ta có:

O M 2 = O K 2 + K M 2

Suy ra:  K M 2 = O M 2 - O K 2  (2)

Mà OH < OK (cmt) (3)

Từ (1), (2) và (3) suy ra: H M 2 > K M 2  hay HM > KM

Đáp án là A

Bài tập 13 trang 106 SGK Toán 9 Tập 1 - H7.net

Câu a: Ta có:

AH=HB⇒OH⊥ABAH=HB⇒OH⊥AB

KC=KD⇒OK⊥CDKC=KD⇒OK⊥CD

Lại có:

AB=CD⇒OH=OKAB=CD⇒OH=OK

⇒ΔHOE=ΔKOE(ch.cgv)⇒ΔHOE=ΔKOE(ch.cgv)

⇒EH=EK(1)⇒EH=EK(1)

Câu b: Ta lại có:

AB=CD⇔AB2=CD2⇔AH=CK(2)AB=CD⇔AB2=CD2⇔AH=CK(2)

Từ (1) và (2):

⇒EH+HA=EK+KC⇔EA=EC

a. Ta có: HA = HB ( gt )

Suy ra : \(OH\perp AB\) ( đường kính dây cung )

Lại có : KC = KD ( gt )

Suy ra : \(OK\perp CD\)( đường kính dây cung )

Mà AB > CD ( gt )

Nên OK > OH ( dây lớn hơn gần tâm hơn )

Áp dụng định lí Pitago vào tam giác vuông OHM ta có :

OM² = OH² + HM²

Suy ra : HM² = OM² – OH² (1)

Áp dụng định lí Pitago vào tam giác vuông OKM ta có:

OM² = OK² + KM²

Suy ra: KM² = OM² – OK² (2)

Mà OH < OK ( cmt ) (3)

Từ (1) (2) và (3) suy ra: HM² > KM² hay HM > KM