a) \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\\ =m^2+6m+9-4m\\ =m^2+2m+9\\ =\left(m+1\right)^2+8>0\forall m\)

Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m.

b) Áp dụng hệ thức Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m\end{matrix}\right.\)

Mà \(x_1^2+x_2^2=6\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\\ \Leftrightarrow\left(m+3\right)^2-2m=6\\ \Leftrightarrow m^2+6m+9-2m=6\\ \Leftrightarrow m^2+4m+3=0\\ \Leftrightarrow\left(m+1\right)\left(m+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)

Vậy \(m\in\left\{-1;-3\right\}\) là các giá trị cần tìm.

a, Ta có: \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\)

                   \(=m^2+6m+9-4m\)

                   \(=m^2+2m+9\)

                   \(=m^2+2m+1+8\)

                   \(=\left(m+1\right)^2+8\)

Lại có:  \(\left(m+1\right)^2\ge0\forall m\Rightarrow\left(m+1\right)^2+8\ge8\forall m\)

Vậy phương trình luôn có 2 nghiêm phân biệt 

b, Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1+x_2=m\end{matrix}\right.\)

Theo bài ra:

 \(x_1^2+x_2^2=6\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)

\(\Leftrightarrow\left(m+3\right)^2-2m=6\)

\(\Leftrightarrow m^2+6m+9-2m=6\)

\(\Leftrightarrow m^2+6m+9-2m-6=0\)

\(\Leftrightarrow m^2+4m+3=0\)

\(\Leftrightarrow m^2+m+3m+3=0\)

\(\Leftrightarrow\left(m^2+m\right)+\left(3m+3\right)=0\)

\(\Leftrightarrow m\left(m+1\right)+3\left(m+1\right)=0\)

\(\Leftrightarrow\left(m+1\right)\left(m+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m+1=0\\m+3=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)

Vậy với m=-1 hoặc m=-3 thì phương trinh trên thỏa mãn hệ thức 

Lời giải:

a.

Từ $x+y=2\Rightarrow y=2-x$. Thay vào PT(2):
$(m+1)x+m(2-x)=7$

$\Leftrightarrow x+2m=7$

$\Leftrightarrow x=7-2m$

$y=2-x=2-(7-2m)=2m-5$

Vậy hpt có nghiệm $(x,y)=(7-2m, 2m-5)(*)$

Nếu $x,y$ có 1 số $\geq 0$, một số $\leq 0$ thì $xy\leq 0< 1$

Nếu $x,y$ cùng $\geq 0$ thì áp dụng BĐT Cô-si:

$2=x+y\geq 2\sqrt{xy}\Rightarrow xy\leq 1$

Vậy tóm lại $xy\leq 1(**)$
Từ $(*); (**)$ suy ra với mọi $m$ thì hpt luôn có nghiệm $x,y$ thỏa mãn $xy\leq 1$

b.

$xy>0$

$\Leftrightarrow (7-2m)(2m-5)>0$

$\Leftrightarrow 7> 2m> 5$

$\Leftrightarrow \frac{7}{2}> m> \frac{5}{2}$

Do $m$ nguyên nên $m=3$

Thử lại thấy đúng.

Lời giải:

a) $x+ay=1\Rightarrow x=1-ay$. Thay vào PT $(2)$ có:

$-a(1-ay)+y=a$

$\Leftrightarrow y(1+a^2)=2a(*)$

Vì $1+a^2\neq 0$ với mọi $a\in\mathbb{R}$ nên PT $(*)$ có nghiệm $y=\frac{2a}{a^2+1}$ duy nhất.

Kéo theo HPT ban đầu có nghiệm $(x,y)$ duy nhất với mọi $a$

b) $y=\frac{2a}{a^2+1}$ nên $x=1-ay=1-\frac{2a^2}{a^2+1}=\frac{1-a^2}{a^2+1}$

Để \(x< 1; y< 1\Leftrightarrow \left\{\begin{matrix} \frac{2a}{a^2+1}< 1\\ \frac{1-a^2}{a^2+1}< 1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a< a^2+1\\ 1-a^2< a^2+1\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} a^2+1-2a>0\\ 2a^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (a-1)^2>0\\ a^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a\neq 1\\ a\neq 0\end{matrix}\right.\)

`a)` Thay `m=\sqrt{3}+1` vào hệ ptr có:

`{(\sqrt{3}x-2y=1),(3x+(\sqrt{3}+1)y=1):}`

`<=>{(3x-2\sqrt{3}y=\sqrt{3}),(3x+(\sqrt{3}+1)y=1):}`

`<=>{((3\sqrt{3}+1)y=1-\sqrt{3}),(\sqrt{3}x-2y=1):}`

`<=>{(y=[-5+2\sqrt{3}]/13),(\sqrt{3}x-2[-5+2\sqrt{3}]/13=1):}`

`<=>{(x=[4+\sqrt{3}]/13),(y=[-5+2\sqrt{3}]/13):}`

`b){((m-1)x-2y=1),(3x+my=1):}`

`<=>{(x=[1-my]/3),((m-1)[1-my]/3-2y=1):}`

`<=>{(x=[1-my]/3),(m-m^2y-1+my-6y=3):}`

`<=>{(x=[1-my]/3),((-m^2+m-6)y=4-m):}`

`<=>{(x=[1-my]/3),(y=[4-m]/[-m^2+m-6]):}`

   Mà `-m^2+m-6` luôn `ne 0`

   `=>AA m` thì đều tìm được `1` giá trị `y` từ đó tìm được `x`

 `=>AA m` thì hệ ptr có `1` nghiệm duy nhất

`c){((m-1)x-2y=1),(3x+my=1):}`

`<=>{(x=[1-my]/3),(y=[4-m]/[-m^2+m-6]):}`

`<=>{(x=(1-m[4-m]/[-m^2+m-6]):3),(y=[4-m]/[-m^2+m-6]):}`

`<=>{(x=[-m^2+m-6-4m+m^2]/[-3m^2+3m-18]),(y=[4-m]/[-m^2+m-6]):}`

`<=>{(x=[-3m-6]/[3(-m^2+m-6)]),(y=[4-m]/[-m^2+m-6]):}`

Ta có: `x-y=[-3m-6]/[3(-m^2+m-6)]-[4-m]/[-m^2+m-6]`

                `=[-3m-6-12+3m]/[-3(m^2-m+6)]`

                `=[-18]/[-3(m^2-m+6)]=6/[(m-1/2)^2+23/4]`

Vì `(m-1/2)^2+23/4 >= 23/4`

`<=>6/[(m-1/2)^2+23/4] <= 24/23`

Hay `x-y <= 24/23`

Dấu "`=`" xảy ra `<=>m-1/2=0<=>m=1/2`

a)   x 2   –   x   –   2   =   0

Có a = 1; b = -1; c = -2 ⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 2.

Vậy tập nghiệm của phương trình là S = {-1; 2}

b) + Đường thẳng y = x + 2 cắt trục Ox tại (-2; 0) và cắt Oy tại (0; 2).

+ Parabol y   =   x 2  đi qua các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4).

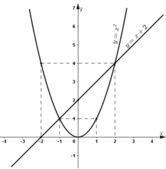
c) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:

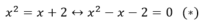
Phương trình (*) chính là phương trình đã giải ở ý (a) Do đó hai nghiệm ở câu (a) chính là hoành độ giao điểm của hai đồ thị

Theo Vi-ét ta có 

x 1 + x 2 = 2 a − 1 x 1 . x 2 = − 4 a − 3 ⇔ 2 ( x 1 + x 2 ) = 4 a − 2 x 1 , x 2 = − 4 a − 3 ⇒ 2 ( x 1 + x 2 ) + x 1 . x 2 = − 5

Vậy hệ thức cần tìm là 2 ( x 1 + x 2 ) + x 1 . x 2 = − 5

Đáp án: D