Giúp mik với
Cảm ơn trước nhá ^^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1)
\(\dfrac{9}{12}+\dfrac{10}{12}=\dfrac{12}{19}\)
\(\dfrac{50}{54}=\dfrac{27}{25}\)
\(\dfrac{16}{24}-\dfrac{9}{24}=\dfrac{7}{24}\)
\(\dfrac{8}{5}x\dfrac{4}{3}=\dfrac{32}{15}\)
____________________________________
Bài 2)
a) \(x=\dfrac{5}{2}-\dfrac{2}{7}\)
\(x=\dfrac{31}{14}\)
b) \(x=\dfrac{6}{7}x\dfrac{4}{5}\)
\(x=\dfrac{24}{35}\)

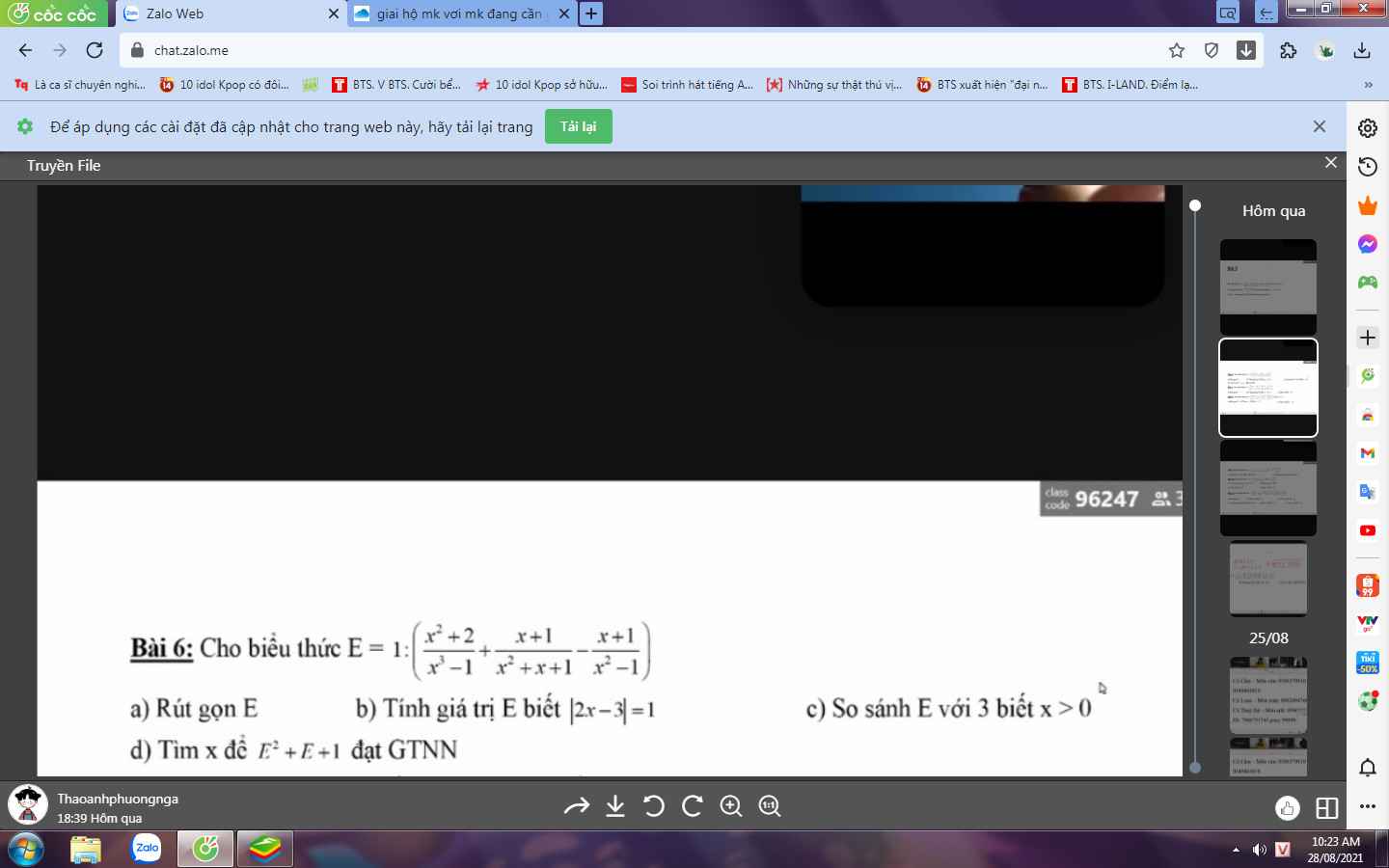
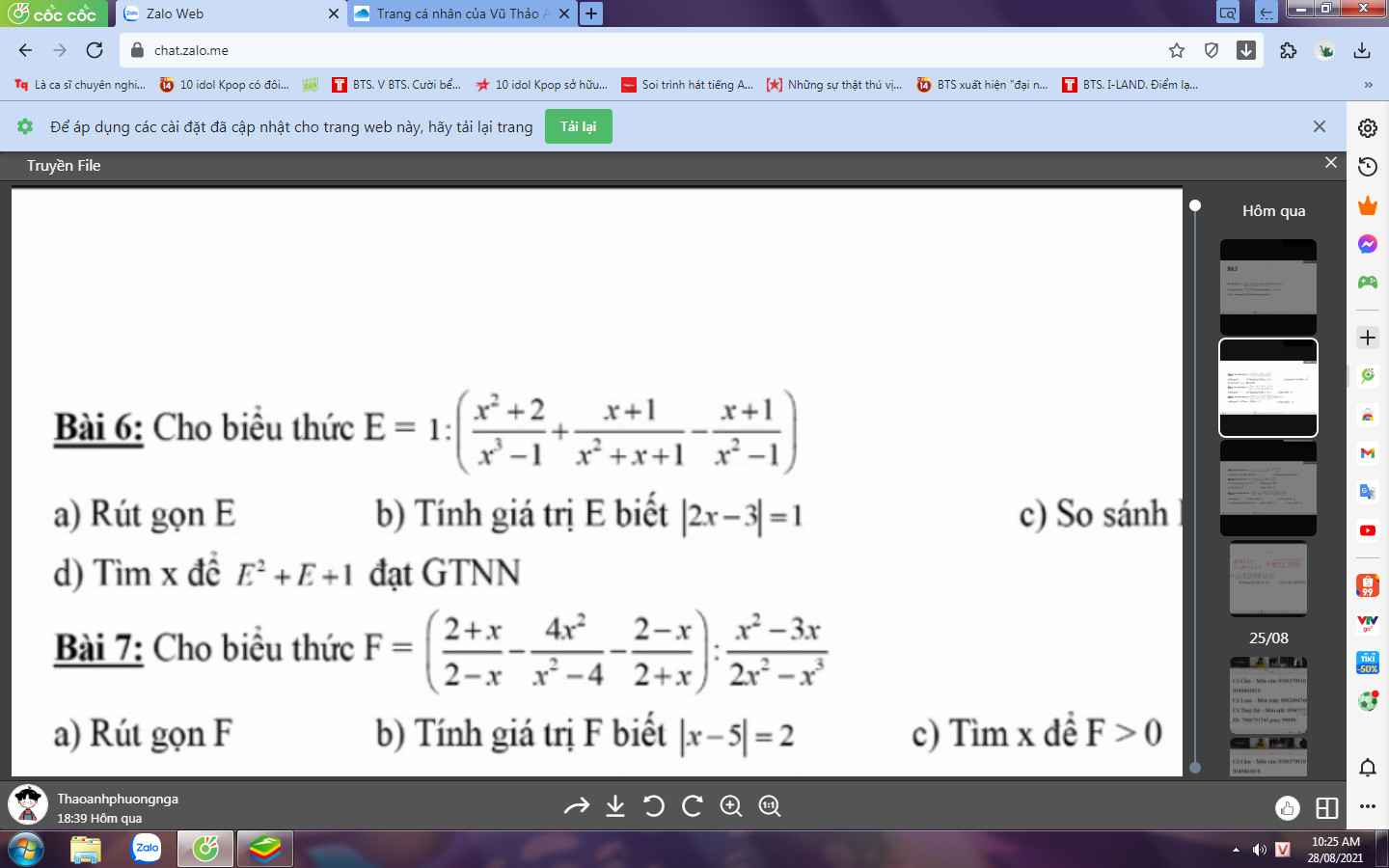
Bài 6:
a: Ta có: \(E=1:\left(\dfrac{x^2+2}{x^3-1}-\dfrac{x+1}{x^2+x+1}-\dfrac{x+1}{x^2-1}\right)\)
\(=1:\left(\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\)
\(=1:\dfrac{x^2+2-x^2+1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-x^2-x+2}\)
\(=\dfrac{-\left(x-1\right)\left(x^2+x+1\right)}{\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-x^2-x-1}{x+2}\)

a. ĐKXĐ: \(x\ge4\)
\(F=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\left(\dfrac{\left(2+x\right)\left(2+x\right)}{\left(2-x\right)\left(2+x\right)}+\dfrac{4x^2}{\left(2-x\right)\left(2+x\right)}-\dfrac{\left(2-x\right)\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{4+4x+x^2+4x^2-4+4x-x^2}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{4x^2+8x}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}=\dfrac{4x\left(x+2\right)x^2\left(2-x\right)}{\left(x+2\right)\left(2-x\right)x\left(x-3\right)}=\dfrac{4x^2}{x-3}\)
b. Ta có \(\left|x-5\right|=2\) \(\Leftrightarrow\left[{}\begin{matrix}x-5=2\\5-x=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\)
* Với \(x=7\), ta có biểu thức \(F=\dfrac{4.7^2}{7-3}=\dfrac{196}{4}=49\)
* Với \(x=3\), ta có biểu thức \(F=\dfrac{4.3^2}{3-3}=\dfrac{36}{0}\), lúc này biểu thức không xác định
c. \(F>0\Leftrightarrow\dfrac{4x^2}{x-3}>0\), vì \(4x^2\ge0\forall x\) nên để \(\dfrac{4x^2}{x-3}>0\) thì \(\left\{{}\begin{matrix}4x^2>0\\x-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x>3\end{matrix}\right.\) \(\Leftrightarrow x>3\)
\(4x^2>0\) thì không tương đương với \(x>0\) mà tương đương với \(x\ne0\)


\(B=|2014-2x|+|2016-2x|\)
\(=|2014-2x|+|2x-2016|\ge|2014-2x+2x-2016|\)
Hay \(B\ge2\)
Dấu"="xảy ra \(\Leftrightarrow\left(2014-2x\right)\left(2x-2016\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}2014-2x\ge0\\2x-2016\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2014-2x< 0\\2x-2016< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x\le2014\\2x\ge2016\end{cases}\left(loai\right)}\)hoặc\(\hept{\begin{cases}2x>2014\\2x< 2016\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1007\\x< 1008\end{cases}}\)
\(\Leftrightarrow1007< x< 1008\)
Vậy \(B_{min}=2\)\(\Leftrightarrow1007< x< 1008\)

Lời giải:
a.
\(G=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{(2x-3)(x+1)-(2x+1)(x-1)}{(x-1)(x+1)}\)
\(=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{-2}{(x-1)(x+1)}=\frac{x^2-4}{x+1}+\frac{2}{x+1}.\frac{(x+1)(x-1)}{-2}\)
\(=\frac{x^2-4}{x+1}-(x-1)=\frac{x^2-4-(x^2-1)}{x+1}=\frac{-3}{x+1}\)
b.
Để $A\in\mathbb{Z}^+$ thì $x+1$ là ước âm của $-3$
$\Rightarrow x+1\in\left\{-1;-3\right\}$
$\Leftrightarrow x\in\left\{-2;-4\right\}$ (tm)
c.
$G< -1\Leftrightarrow \frac{-3}{x+1}+1< 0$
$\Leftrightarrow \frac{x-2}{x+1}< 0$
$\Leftrightarrow x-2<0< x+1$ hoặc $x-2>0>x+1$
$\Leftrightarrow -1< x< 2$ (chọn) hoặc $-1> x>2$ (loại)
Vậy $-1< x< 2$ và $x\neq 1$
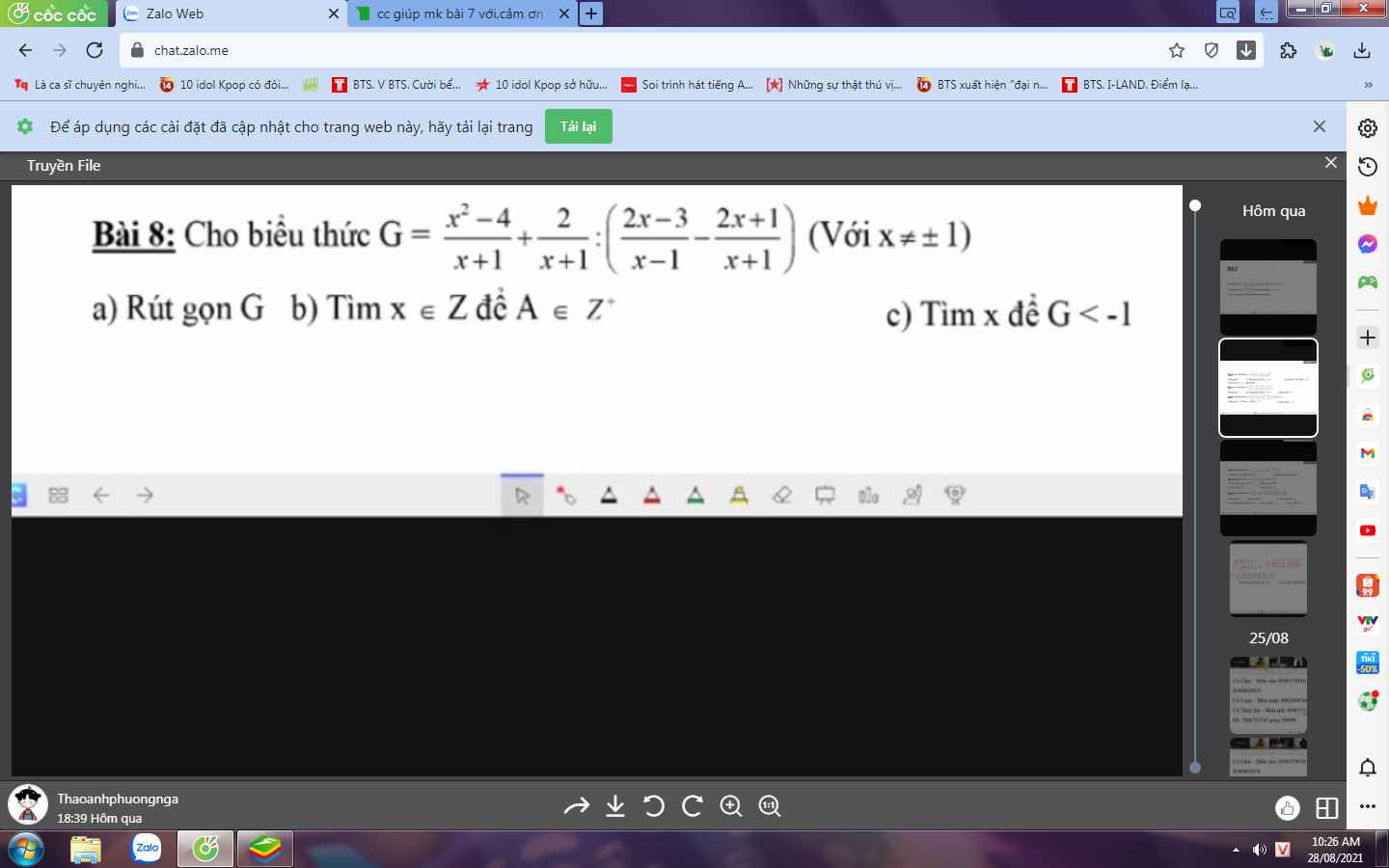
Bài 8:
a: Ta có: \(G=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\left(\dfrac{2x-3}{x-1}-\dfrac{2x+1}{x+1}\right)\)
\(=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\dfrac{2x^2+2x-3x-3-2x^2+2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{2}{x+1}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{-x+1}{1}\)
\(=\dfrac{x^2-4-\left(x-1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x^2-4-x^2+1}{x+1}\)
\(=-\dfrac{3}{x+1}\)

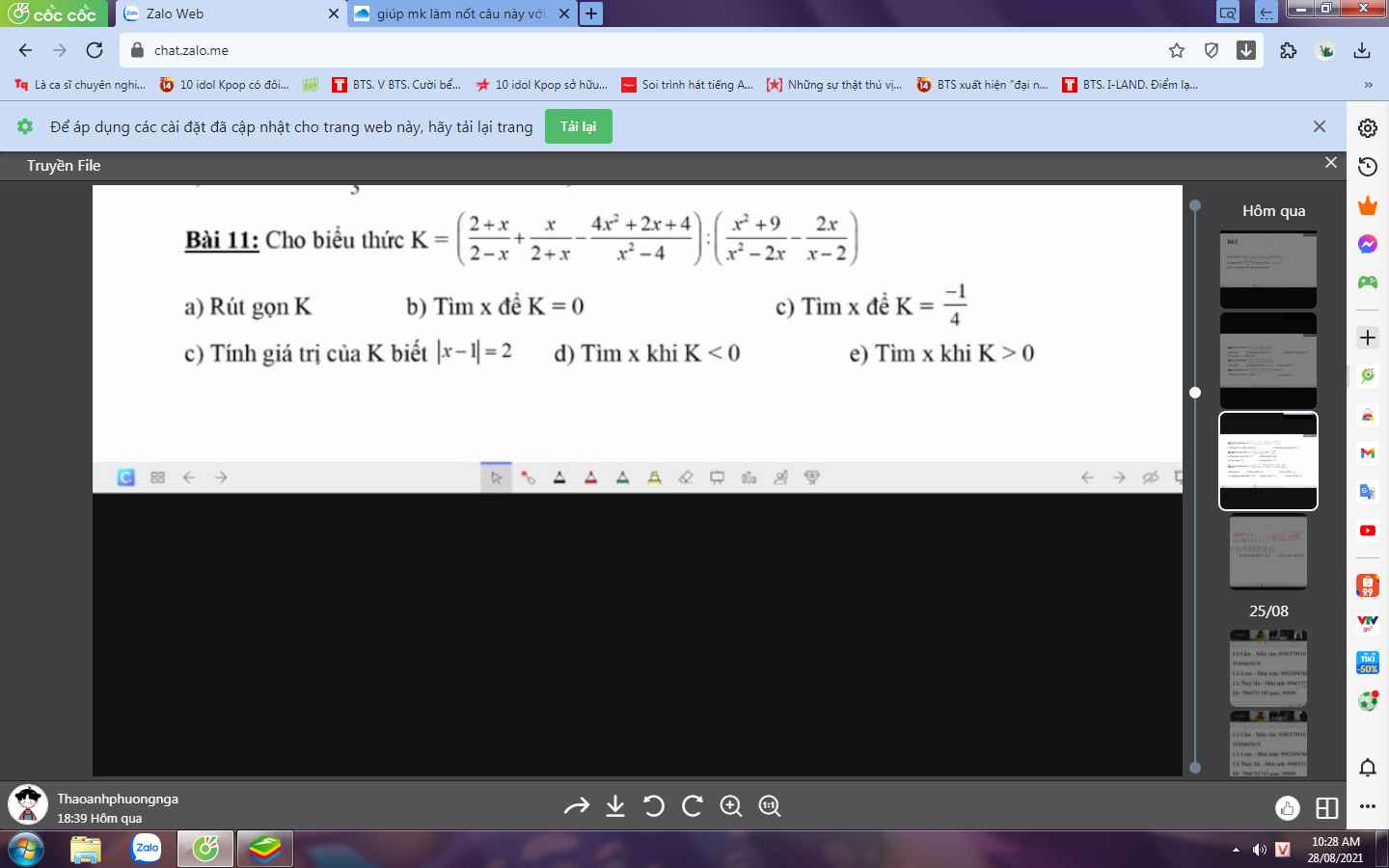
a: Ta có: \(K=\left(\dfrac{2+x}{2-x}+\dfrac{x}{2+x}-\dfrac{4x^2+2x+4}{x^2-4}\right):\left(\dfrac{x^2+9}{x^2-2x}-\dfrac{2x}{x-2}\right)\)
\(=\dfrac{-x^2-4x-4+x^2-2x-4x^2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2+9-2x^2}{x\left(x-2\right)}\)
\(=\dfrac{-4x^2-8x-8}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-2\right)}{-x^2+9}\)
\(=\dfrac{-4\left(x^2+2x+1\right)}{x+2}\cdot\dfrac{x}{-\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{-4x\left(x+1\right)^2}{-\left(x-3\right)\left(x+3\right)\left(x+2\right)}\)

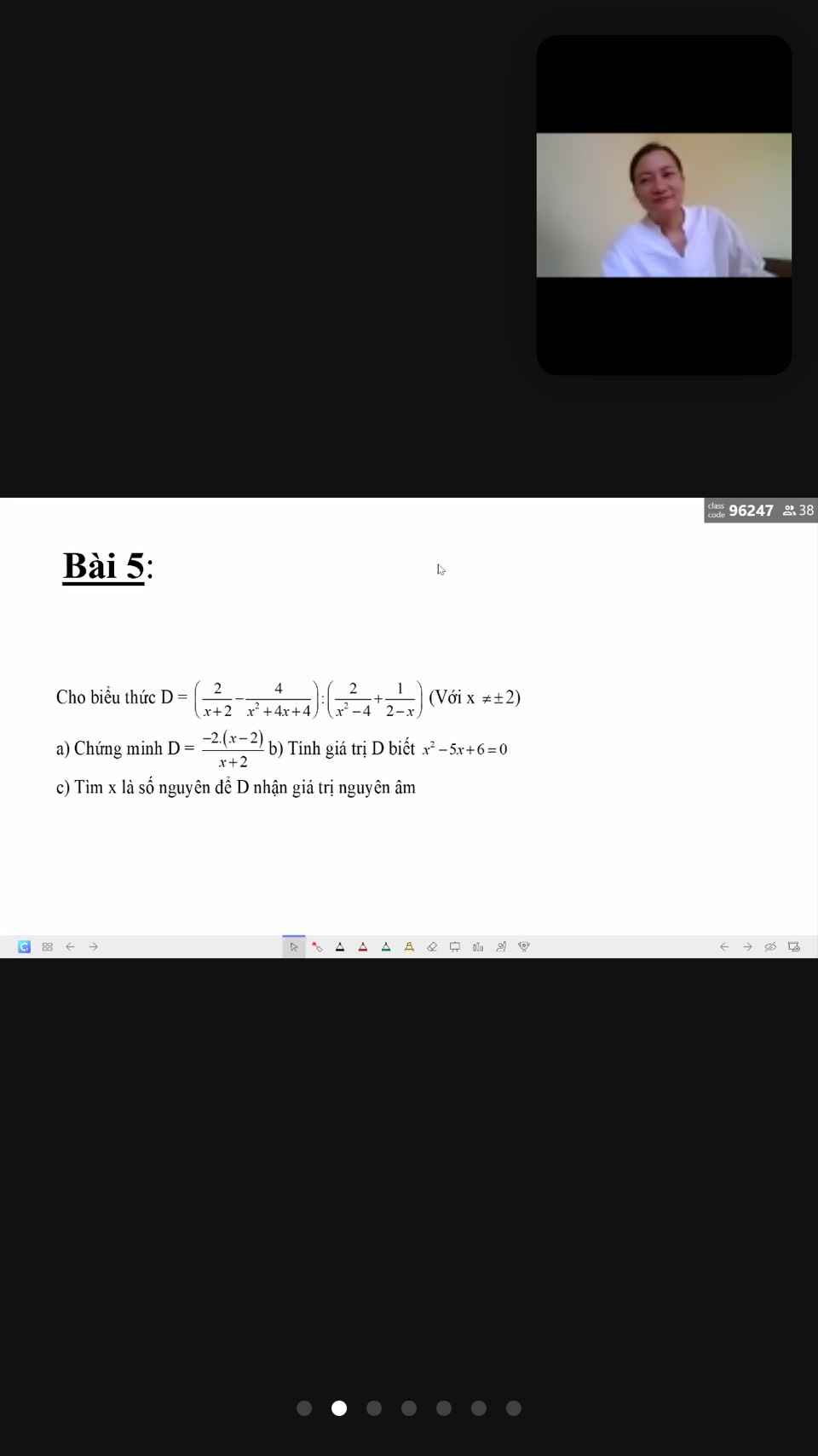
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)
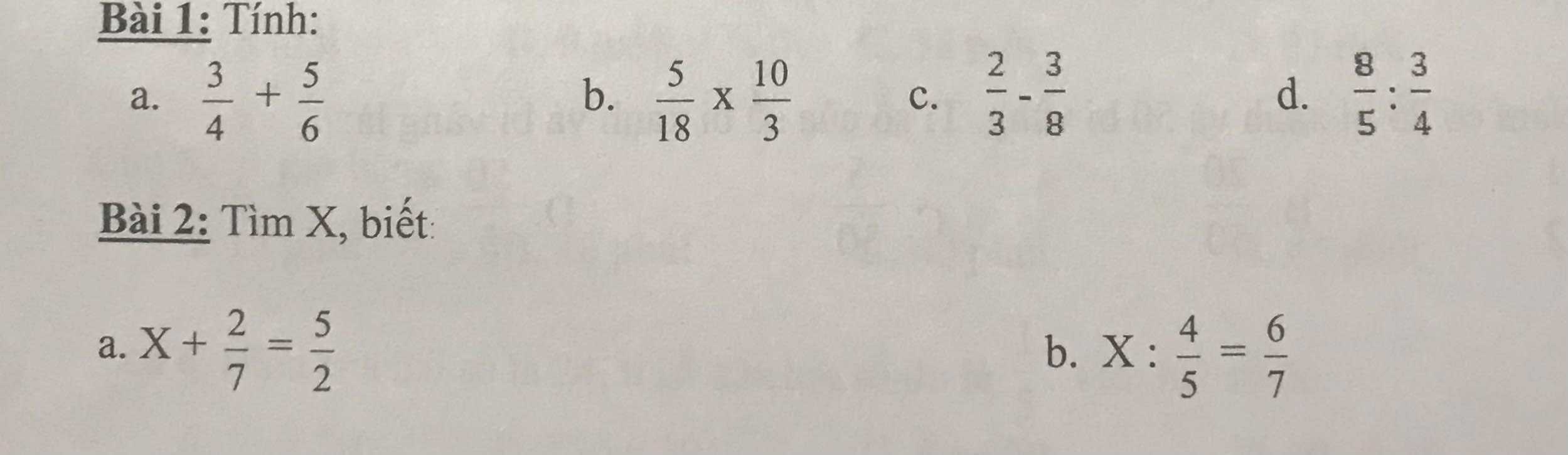


 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
dO2\H2=32\2=16
dN2\H2=28\2=14
dCO2\H2=44\2=22
B)
dO2\kk=32\29=1,1
dN2\kk=28\29=0,9655
dCO2\kk=44\29=1,517