Cho hàm số: \(y=\dfrac{2-x}{x+1}\). Tìm khoảng đồng biến, nghịch biến của hàm số đã cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Lời giải:
a.
$y'=\frac{2(1-x^2)}{(x^2+1)^2}>0, \forall x\in (0; 1)$
$\Rightarrow y$ đồng biến trên khoảng $(0;1)$
b.
Với mọi $x>1$ thì $y'=\frac{2(1-x^2)}{(x^2+1)^2}< 0$
$\Rightarrow$ hàm số nghịch biến trên $(1;+\infty)$

1: TXĐ: D=R\{3}
\(y=\dfrac{x^2-6x+10}{x-3}\)
=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)
Đặt y'<=0
=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)
=>\(x^2-6x+8< =0\)
=>(x-2)(x-4)<=0
=>2<=x<=4
Vậy: Khoảng đồng biến là [2;3) và (3;4]

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

a: \(y'=\dfrac{\left(x-1\right)'\left(x+1\right)-\left(x-1\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x+1}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}>0\)
=>Hàm số luôn đồng biến khi x<>-1
vậy: Các khoảng đồng biến là \(\left(-\infty;-1\right);\left(-1;+\infty\right)\)
b: \(y'=\dfrac{\left(2x+1\right)'\left(8x-1\right)-\left(2x+1\right)\left(8x-1\right)'}{\left(8x-1\right)^2}\)
\(=\dfrac{2\left(8x-1\right)-8\left(2x+1\right)}{\left(8x-1\right)^2}\)
\(=\dfrac{16x-2-16x-8}{\left(8x-1\right)^2}=-\dfrac{10}{\left(8x-1\right)^2}< 0\)
=>Hàm số nghịch biến khi x<>1/8
Vậy: Các khoảng nghịch biến là \(\left(-\infty;\dfrac{1}{8}\right);\left(\dfrac{1}{8};+\infty\right)\)

\(a,\) Hàm số đồng biến \(\Leftrightarrow a>0\Leftrightarrow\dfrac{m+1}{2m-3}>0\left(dk:m\ne\dfrac{3}{2}\right)\Leftrightarrow m+1>0\Leftrightarrow m>-1\)
\(\Leftrightarrow\left[{}\begin{matrix}m>-1\\m\ne\dfrac{3}{2}\end{matrix}\right.\)
\(b,\) Hàm số nghịch biến \(\Leftrightarrow a< 0\Leftrightarrow\dfrac{m+1}{2m-3}< 0\left(dk:m\ne\dfrac{3}{2}\right)\Leftrightarrow m+1< 0\Leftrightarrow m< -1\)


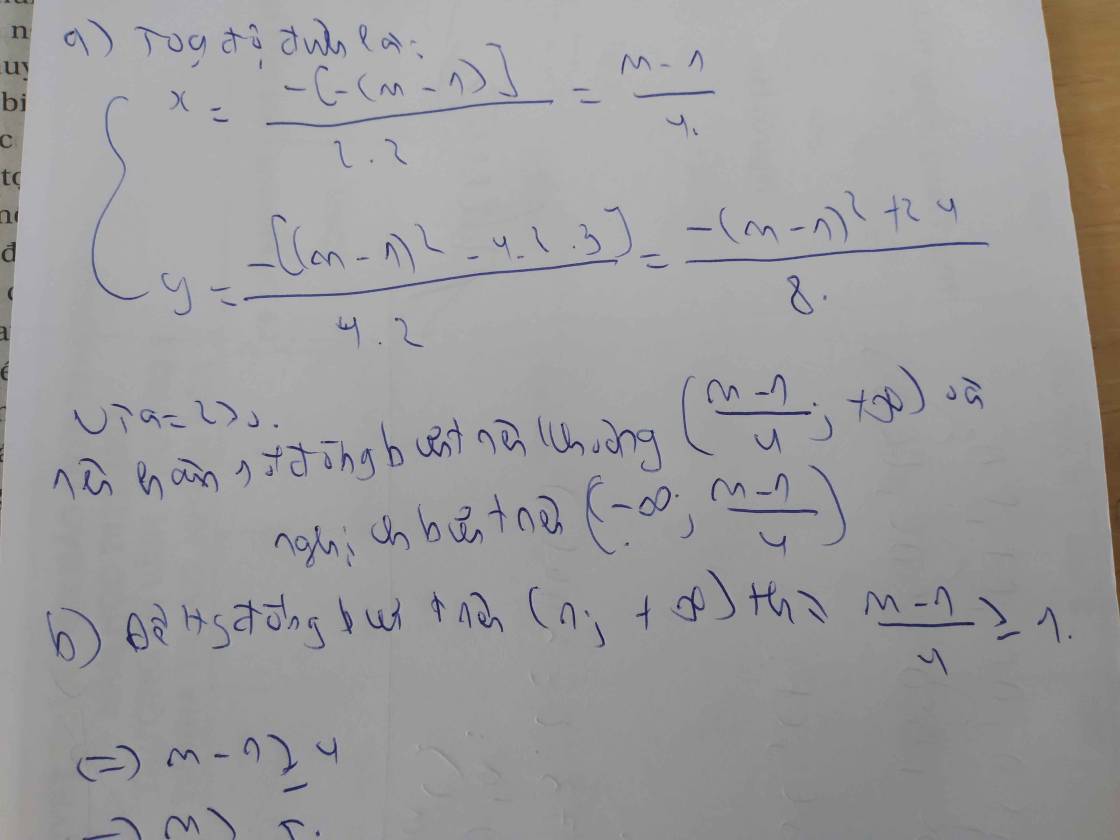

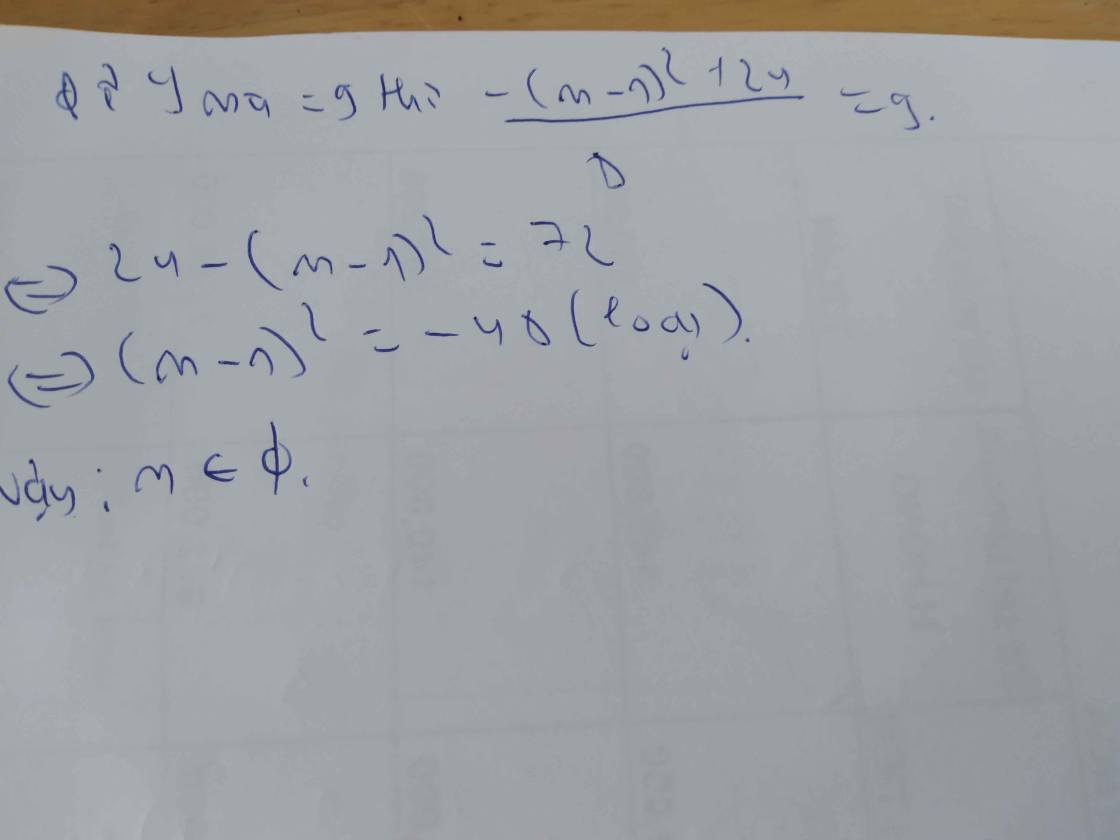
B