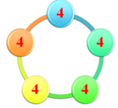
người ta viết 7 số hữu tỉ trên một vòng tròn tìm các số đó biết rằng tích của hai số bất kì cạnh nhau bằng 16 cũng hỏi như trên đối với n số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
Đỗ Thanh Hải
CTVVIP
14 tháng 5 2021
a) Gọi 7 số đó là: a1, a2, a3 ..... a7 (đk các số khác 0)
Ta có a1.a2 = a2.a3 => a1=a3
Tương tự a2 = a4, a3=a5,.......
=> Các số đều bằng nhau
mà 2 số bất kì có tích = 16
=> Các số có thể là 4 hoặc -4
PT
15 tháng 5 2021
Giả sử n là số lẻ
Gọi n số đã cho là \(a_1;a_2;...;a_n\)
Giả sử n số này được viết trên 1 vòng tròn theo thứ tự như trên.
Ta có \(a_1.a_2=a_2.a_3=...=a_{n-1}.a_n\\
\Rightarrow a_1=a_3=...=a_n;a_2=a_4=...a_{n-1}\)
Lại có \(a_n.a_1=16\Leftrightarrow a_1^2=16\Rightarrow a_1=\pm4\)
* Nếu a1 = 4 thì an = 4
* Nếu a1 = -4 thì an = -4
Vậy các số có thể là 4 hoặc -4
H
10 tháng 7 2021
Gọi 10 số đó là : \(a_1,a_2,...,a_{10}\in Q\)
Ta có : \(a_1a_2=a_2a_3=...=a_9a_{10}=a_{10}a_1=25\)
Suy ra \(a_1,a_2,...,a_{10}\ne0\)
Mà \(a_{1}a_{2} = a_{2} a_{3} \Rightarrow a_{1}=a_{3}\)
Tương tự : \(a_1=a_3=a_5=a_7=a_9;a_2=a_4=a_6=a_8=a_{10}\)
Vậy suy ra \(a_1=a_3=a_5=a_7=a_9=k\\ a_2=a_4=a_6=a_8=a_{10}=\dfrac{25}{k}\left(k\in Q\right)\)