a, Vì \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\) nên AEHD là hcn

Do đó AH=DE

b, Vì \(\widehat{HAB}=\widehat{MCA}\) (cùng phụ \(\widehat{CAH}\))

Mà \(\widehat{MCA}=\widehat{MAC}\) (do \(AM=CM=\dfrac{1}{2}BC\) theo tc trung tuyến ứng ch)

Vậy \(\widehat{HAB}=\widehat{MAC}\)

c, Gọi O là giao AM và DE

Vì AEHD là hcn nên \(\widehat{HAB}=\widehat{ADE}\Rightarrow\widehat{MAC}=\widehat{ADE}\)

Mà \(\widehat{ADE}+\widehat{AED}=90^0\left(\Delta AED\perp A\right)\) nên \(\widehat{MAC}+\widehat{ADE}=90^0\)

Xét tam giác AOE có \(\widehat{AOE}=180^0-\left(\widehat{MAC}+\widehat{ADE}\right)=90^0\)

Vậy AM⊥DE tại O

Xét tứ giác ADHE có

\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)

=>ADHE là hình chữ nhật

=>\(\widehat{AED}=\widehat{AHD}\)

mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)

nên \(\widehat{AED}=\widehat{ABC}\)

ΔABC vuông tại A

mà AM là đường trung tuyến

nên MA=MC=MB

MA=MC

=>ΔMAC cân tại M

=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)

\(\widehat{MAC}+\widehat{AED}=\widehat{ACB}+\widehat{ABC}=90^0\)

=>AM vuông góc DE

a: Xét tứ giác ADME có 

\(\widehat{AEM}=\widehat{ADM}=\widehat{EAD}=90^0\)

Do đó: ADME là hình chữ nhật

Suy ra: AM=DE

Bạn tham khảo bài làm ở đường link phía dưới nhé:

Câu hỏi của Nguyễn Desmond - Toán lớp 8 - Học toán với OnlineMath

Xét tứ giác ADHE có

\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

=>ADHE là hình chữ nhật

=>\(\widehat{AED}=\widehat{AHD}\)

AM\(\perp\)DE

=>\(\widehat{AED}+\widehat{MAC}=90^0\)

mà \(\widehat{AED}=\widehat{AHD}\left(cmt\right)\) 

và \(\widehat{AHD}=\widehat{ABH}\left(=90^0-\widehat{HAB}\right)\)

nên \(\widehat{ABH}+\widehat{MAC}=90^0\)

mà \(\widehat{ABH}+\widehat{MCA}=90^0\)(ΔABC vuông tại A)

nên \(\widehat{MAC}=\widehat{MCA}\)

=>MA=MC

\(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)

\(\widehat{MCA}+\widehat{MBA}=90^0\)(ΔABC vuông tại A)

mà \(\widehat{MAC}=\widehat{MCA}\)

nên \(\widehat{MAB}=\widehat{MBA}\)

=>MA=MB

mà MA=MC

nên MB=MC

=>M là trung điểm của BC

( Hình em tự vẽ nhé! )

Lấy O là giao điểm DE và HA

+ Xét tứ giác ADHE có:

\(\widehat{HDA}=\widehat{DAE}=\widehat{AEH}=90^o\)

=> ADHE là hình chữ nhật

=> O là trung điểm AH (t/c)

     O là trung điểm DE (t/c)

=> OA = OH = OD = OE 

=> ΔAOE cân tại O

=> \(\widehat{OAE}=\widehat{OEA}\left(tc\right)\)

+ Xét ΔABH vuông tại H

=> \(\widehat{BAH}+\widehat{ABH}=90^o\)

Mà \(\widehat{BAH}+\widehat{CAH}=90^o\)

=> \(\widehat{ABH}=\widehat{CAH}\)

Mà \(\widehat{CAH}=\widehat{OEH}\)

\(\widehat{ABH}=\widehat{AEO}\)

+ Xét ΔADE và ΔACB có:

\(\widehat{DAE}=\widehat{CAB}\left(=90^o\right)\)

\(\widehat{AED}=\widehat{ABC}\)

=> ΔADE \(\sim\) ΔACB (g.g)

=> \(\widehat{ADE}=\widehat{ACB}\left(2gtu\right)\)

Lấy I là giao điểm AM và DE 

+ Xét ΔAIE vuông tại I 

=> \(\widehat{IAE}+\widehat{IEA}=90^o\)

Mà \(\widehat{BAM}+\widehat{MAC}=90^o\)

=> \(\widehat{IEA}=\widehat{MAB}\)

Mà \(\widehat{IEA}=\widehat{ABC}\)

=> \(\widehat{ABC}=\widehat{BAM}\)

=> ΔABM cân tại M

=> MA = MB (t/c)

+ Xét ΔAID vuông tại I

=> \(\widehat{IDA}+\widehat{IAD}=90^o\)

Mà \(\widehat{IAD}+\widehat{MAC}=90^o\)

=> \(\widehat{IDA}=\widehat{MAC}\)

Mà \(\widehat{IDA}=\widehat{ACM}\)

=> \(\widehat{MAC}=\widehat{ACM}\)

=> ΔMAC cân tại M

=> MA = MC (t/c)

Mà MA = MB 

=> MB = MC

=> M là trung điểm BC.

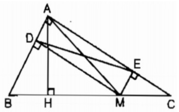
Xét tứ giác ADME, ta có:

∠ A = 90 0  (gt)

MD ⊥ AB (gt)

⇒  ∠ (MDA ) =  90 0

ME ⊥ AC (gt)

⇒  ∠ (MEA ) =  90 0

Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)

⇒ AM = DE ( tính chất hình chữ nhật)

a) Xét tứ giác AEMF có 

\(\widehat{AFM}=90^0\)(gt)

\(\widehat{AEM}=90^0\)(gt)

\(\widehat{FAE}=90^0\)(gt)

Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

Suy ra: AM=EF(Hai đường chéo của hình chữ nhật AFME)

b) Gọi O là giao điểm của AM và EF

Ta có: AMFE là hình chữ nhật(cmt)

nên Hai đường chéo AM và EF cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)

mà O là giao điểm của AM và EF(gt)

nên O là trung điểm của AM; O là trung điểm của EF

Ta có: ΔAHM vuông tại H(gt)

mà HO là đường trung tuyến ứng với cạnh huyền AM(O là trung điểm của AM)

nên \(HO=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

mà AM=EF(cmt)

nên \(HO=\dfrac{EF}{2}\)

Xét ΔHFE có 

HO là đường trung tuyến ứng với cạnh EF(O là trung điểm của EF)

\(HO=\dfrac{EF}{2}\)(cmt)

Do đó: ΔHFE vuông tại H(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)