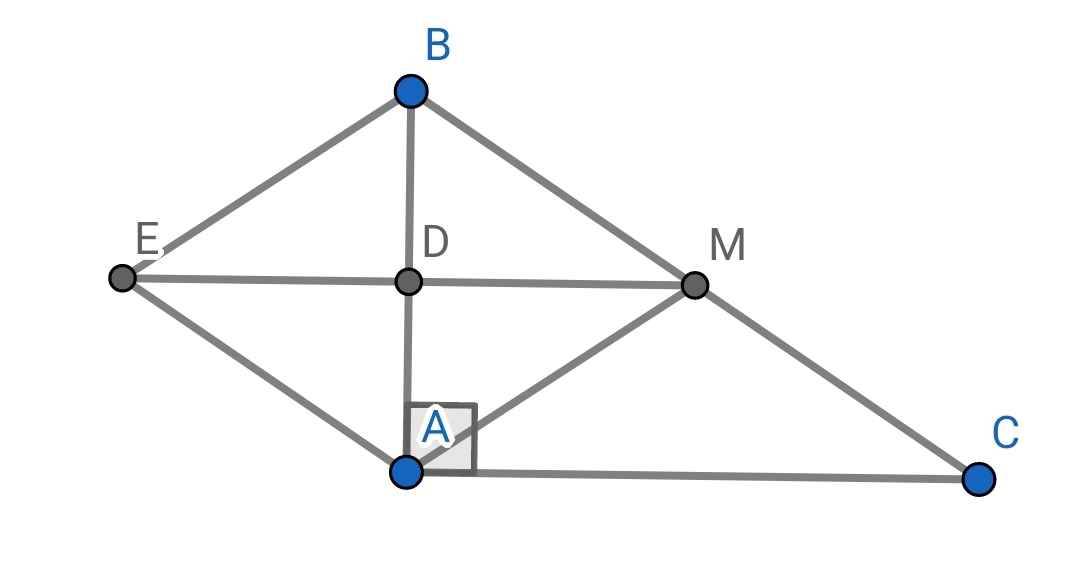
Cho tam giác ABC cân tại A, trung tuyến AM. D trung điểm AC. E là điểm đối xứng M qua D.
a, Tứ giác AECM là hình gì? Vì sao
b, Tứ giác AEMB là hình gì? Vì sao
c, Tìm đi của tam giác ABC để tứ giác AECM là hình vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2021
a: Xét tứ giác AMCE có
D là trung điểm của AC
D là trung điểm của ME
Do đó: AMCE là hình bình hành
mà MA=MC
nên AMCE là hình thoi
9 tháng 1 2023
a: Xét tứ giác AECM có
N là trung điểm chung của AC và EM
nên AECM là hình bình hành
c: Để AECM là hình vuông thì góc CAM=45 độ và CM=MA
=>ΔBAC vuông cân tại C
26 tháng 12 2021
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
26 tháng 12 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
7 tháng 1 2023
a: Xét ΔCAB có CE/CA=CM/CB
nên ME//ABvà ME=AB/2
=>ME//AD và ME=AD
=>ADME là hình bình hành
mà góc DAE=90 độ
nên ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AM=DE
c: BC=15cm
=>AM=15/2=7,5cm
=>DE=7,5cm
d: Xét tứ giác AMCF có
E là trung điểm chung của AC và MF
MA=MC
Do đó: AMCF là hình thoi
KV
29 tháng 12 2022
a) Do E và M đối xứng qua D
⇒ D là trung điểm EM
Do D là trung điểm AB
M là trung điểm BC (AM là đường trung tuyến)
⇒DM là đường trung bình của ∆ABC
⇒DM // AC
Mà AC vuông góc AB
⇒DM vuông góc AB
Hay EM vuông góc AB tại D
⇒AB là đường trung trực của EM
Hay E và M đối xứng qua AB
b) Do D là trung điểm AB (gt)
D là trung điểm EM (cmt)
⇒AEBM là hình bình hành
Mà AB vuông góc EM (cmt)
⇒AEBM là hình thoi
c) Do BC = 4 (cm)
⇒BM = BC : 2
= 4 : 2
= 2 (cm)
Chu vi AEBM:
2 . 4 = 8 (cm)
Xét tam giác ABC cân tại A có AM là trung tuyến
=> AM đồng thời là đường cao
=> AM ⊥ BC hay AMC = 900 (1)
Xét tứ giác AECM có AC giao ME tại D
mà D đồng thời là trung điểm của AC và ME
=> tứ giác AECM là hình bình hành (2)
Từ (1) và (2) => AECM là hình chữ nhật
b) Vì AECM là hình chữ nhật
=> AE // BC (3)
Xét tam giác ABC có D là trung điểm của AC; M là trung điểm của BC
=> DM là đường trung bình của tam giác ABC
=> DM // AB (4)
Từ (3) và (4) => AEMB là hình bình hành ( đpcm )
c) ko hiểu đề :))
c,
Hình chữ nhật AECM là hình vuông khi \(AC\perp EM\Rightarrow AC\perp AB\) (vì EM // AB ) \(\Rightarrow\widehat{BAC}=90^0\)
Vậy tam giác ABC vuông cân tại A thì AECM là hình vuông