giúp mik bài 1 câu c
và bài 2 câu b,c với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


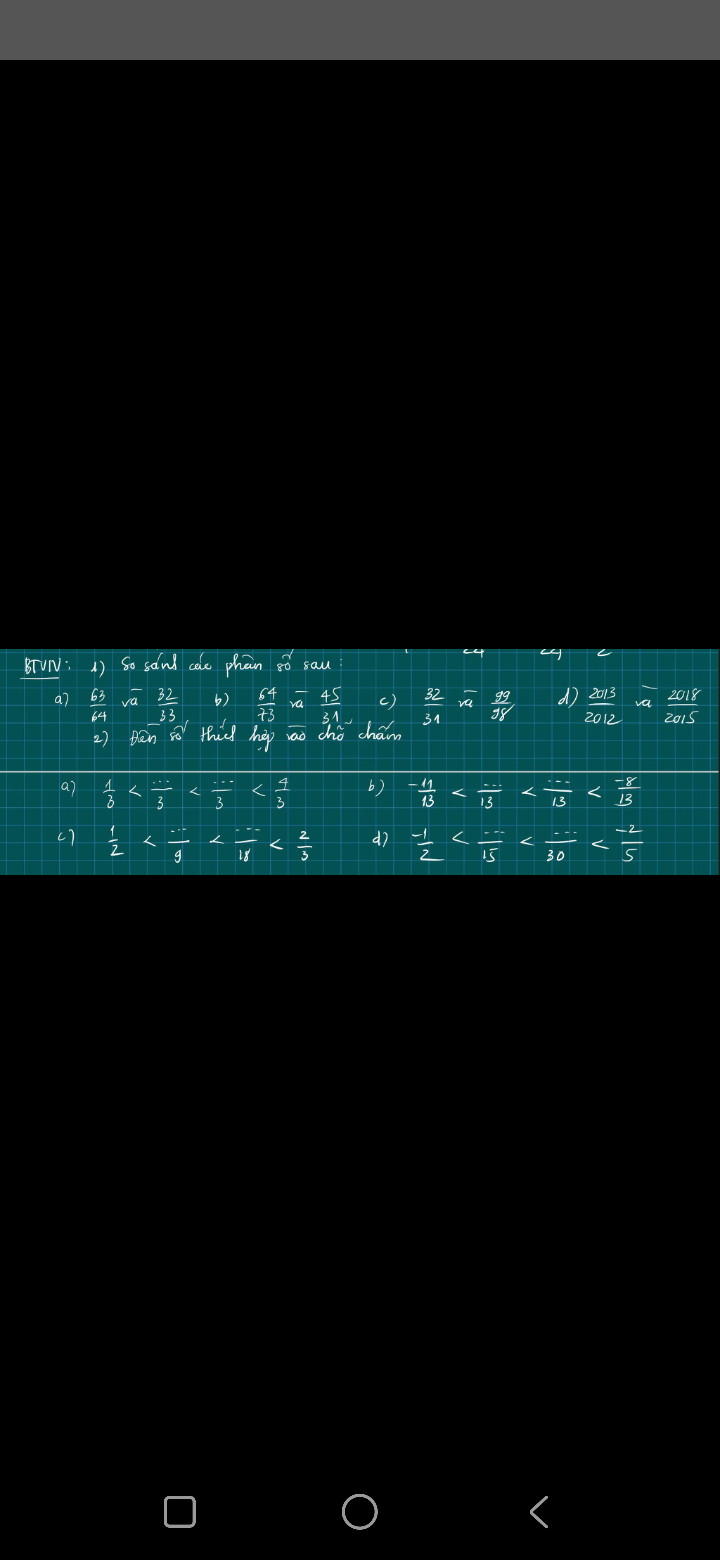
c: Gọi hai số cần tìm là x,y
Theo đề, ta có: \(9< 2x< y< 12\)
=>2x=10 và y=11
=>x=5 và y=11
d: Gọi hai số cần tìm là x,y
Theo đề, ta có: \(-15< 2x< y< -12\)
=>2x=-14 và y=-13
=>x=-7 và y=-13

a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

Bài 1:
a: Xét tứ giác BEDF có
ED//BF
ED=BF
Do đó: BEDF là hình bình hành
Suy ra: BE=DF
c: ta có: BEDF là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường
mà AC và BD cắt nhau tại trung điểm của mỗi đường
nên AC,BD,EF đồng quy

Bài 4:
a, F(\(x\)) = m\(x\) + 3 có nghiệm \(x\) = 2
⇔ F(2) = 0 ⇔ m.2 + 3 = 0
2m = -3
m = - \(\dfrac{3}{2}\)
b, F(\(x\)) = m\(x\) - 5 có nghiệm \(x\) = 3 ⇔ F(3) = 0
⇔3m - 5 = 0 ⇒ m = \(\dfrac{5}{3}\)
c, F(\(x\)) = \(x^2\) + a\(x\) + b có 2 nghiệm phân biệt \(x\) = 1; \(x\) = 0
⇔ \(\left\{{}\begin{matrix}0+0+b=0\\1+a+b=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}b=0\\a=-1\end{matrix}\right.\)

Câu 23:
a: Ta có: \(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{5\sqrt{x}}{\sqrt{x}+3}=\dfrac{22}{x-9}\)
Suy ra: \(x+5\sqrt{x}+6-5x+15\sqrt{x}-22=0\)
\(\Leftrightarrow-4x+20\sqrt{x}-16=0\)
\(\Leftrightarrow x-5\sqrt{x}+4=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=16\left(nhận\right)\end{matrix}\right.\)


1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)



 giúp mik câu c bài 3 và hết bài 4 vs ạ
giúp mik câu c bài 3 và hết bài 4 vs ạ

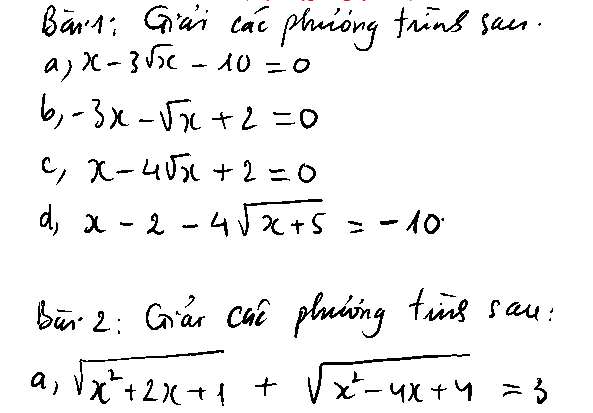
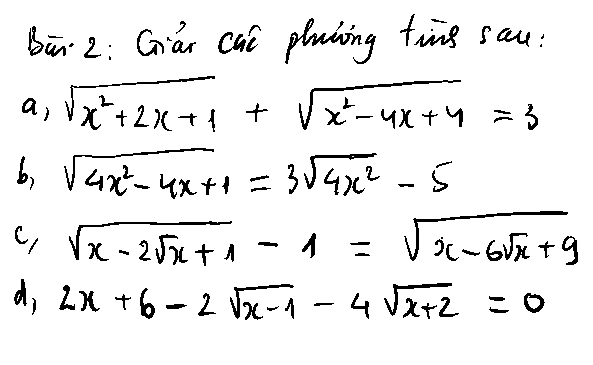
Câu 1:
Quy ước gen: A hạt vàng. a hạt xanh
c) ta sẽ cho cây đậu Hà Lan hạt vàng đó đi lai phân tích
- Nếu đời con đồng tính thì cá thể trội đem lai là thuần chủng.
- Nếu đời con có sự phân tính thì cá thể trội đem lai không thuần chủng
Bài 2:
Quy ước gen: A tóc xoăn. a tóc thẳng
B mắt nâu. b mắt xanh
b) kiểu gen người con trai tíc thẳng mắt xanh: aabb
-> mỗi bên P cho ra 1 loại giao tử : ab
Mà kiểu hình P:+ bố tóc xoăn mắt nâu -> kiểu gen : AaBb
+mẹ tóc thẳng mắt nâu -> kiểu gen: aaBb
c) giao tử gen bố: AB,Ab,aB,ab
Giao tử gen mẹ : aB,ab