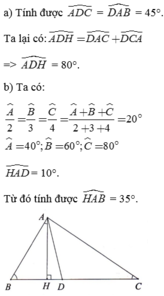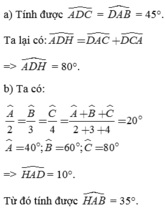Cho tam giác ABC có góc B= \(70^0\), góc C=\(40^0\). Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H ϵ BC). Tính góc BAC, góc ADH, góc HAD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A) Xét tam giác ABC có: ABC+ACB+BAC=180*
hay:70*+30*+BAC=180*
=> BAC=180*-70*-30*=80*
Vậy BAC=80*
b) Vì AD là tia phân giác của góc BAC:
nên góc\(BAD=DAC=\frac{BAC}{2}=\frac{80}{2}=40^0\)
Xét tam giác ADC có: góc DAC+ACD+ADC=180*
hay: 40*+30*+ADC=180*
=> ADC+180*-40*-30*=110*
Vì ADC kề bù với góc ADH:
nên: ADC+ADH=180*
hay: 110*+ADH=180*
=> ADH=180*-110*
Vậy ADH=70*
c) Vì AH vuông góc với BC nên góc AHD=90*
Xét tam giác AHD có: AHD +ADH+HAD=180*
hay: 90*+70*+HAD=180*
=> HAD=180*-90*-70*=20*
Vậy HAD=70*
![]()
![]()
a. Ta có Góc A+B+C=180o ( tổng các góc trong tam giác luôn bằng 180o)
Suy ra: Góc A= 180o- Góc B-C= 180o - 70o- 30o= 80o
b. Vì AD là tia phân giác của góc A nên ta có:
Góc D=A:2=80o:2=40o
Mik chỉ làm đc bằng này thôi, xl nha.

Ta có
góc A + góc B + góc C = 1800
=> góc a + 700 + 300 = 1800
=> góc A = 800