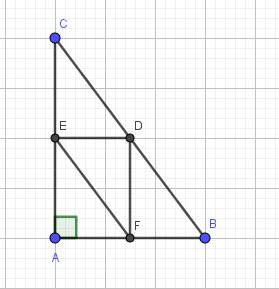
Cho tam giác ABC. D là 1 điểm bất kì trên cạnh BC. Vẽ DE song song với AC. DF song song với AB (E thuộc AB, E thuộc AC)
a. Tứ giác AEDF là hình gì? Vì sao?
b. gọi I là trung điểm của AD. Chứng minh 3 điểm I, E, F thẳng hàng
c. Nếu tam giác ABC có góc A= 90º thì tứ giác AEDF là hình gì? vì sao?
Khi đó điểm D nằm ở vị trí nào trên cạnh BC để đoạn thẳng EF có độ dài nhỏ nhất?
d. Khi điểm D di chuyển trên cạnh BC thì trung điểm I của AD di chuyển trên đường nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành

a/
DE//AB=> DE//AF
DF//AC=>DF//AE
=> AEDF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Hình bình hành AEDF có \(\widehat{A}=90^o\) => AEDF là hình chữ nhật
b/
DE//AB
DB=DC (1)
=> FA=FC (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại (2)
Từ (1) và (2) => DE là đường trung bình của ABC
\(\Rightarrow DE=\dfrac{BC}{2}=FB=FC\) (3)
DE//AB=> DE//FB (4)
Từ (3) và (4) => BFED là hình bình hành (Tứ giác có cặp cạnh đối // và bằng nhau là hbh)
a) Do DE // AB (gt)
\(AC\perp AB\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow DE\perp AC\)
\(\Rightarrow\widehat{DEA}=90^0\)
Do DF // AC (gt)
\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow DF\perp AC\)
\(\Rightarrow\widehat{DFA}=90^0\)
Tứ giác AEDF có:
\(\widehat{EAF}=\widehat{DEA}=\widehat{DFA}=90^0\)
\(\Rightarrow AEDF\) là hình chữ nhật
b) Do D là trung điểm BC (gt)
DF // AB (gt)
\(\Rightarrow F\) là trung điểm của AB
\(\Rightarrow FA=FB\)
Do AEDF là hình bình hành
\(\Rightarrow DE=AF\)
\(\Rightarrow DE=FB\)
Lại có:
DE // AB
\(\Rightarrow\) DE // FB
Tứ giác BFED có:
DE // FB (cmt)
DE = FB (cmt)
\(\Rightarrow BFED\) là hình bình hành

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A

Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật

Xét tứ giác AFDE có
DE//AF
AE//DF
Do đó: AFDE là hình bình hành
Suy ra: hai đường chéo AD và FE cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của AD
nên I là trung điểm của FE
hay F và E đối xứng nhau qua I
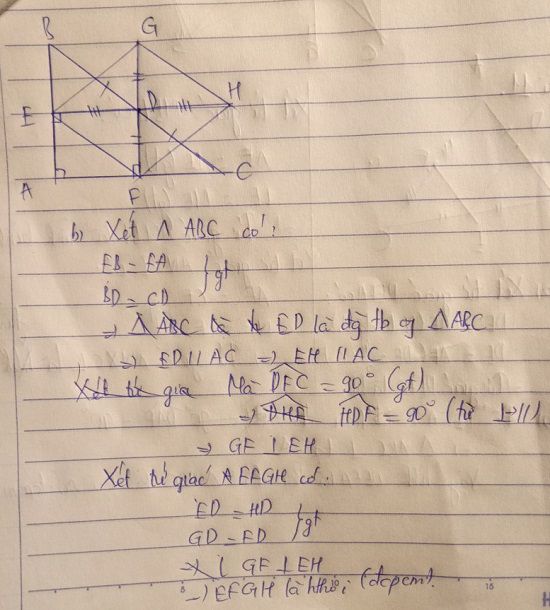

F thuộc AC nha