giúp j vậy bn

Đề ?_?

@Cpr

#Forever

Bài nào v ạ

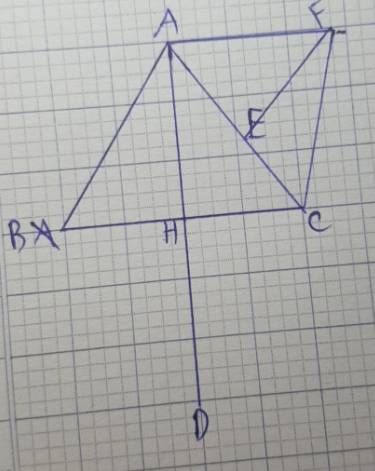
a: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

Xét tứ giác ABDC có

H là trung điểm chung của AD và BC

nên ABDC là hình bình hành

Hình bình hành ABDC có AB=AC

nên ABDC là hình thoi

b: H là trung điểm của BC

=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)

ΔAHB vuông tại H

=>\(AH^2+HB^2=AB^2\)

=>\(AH^2=5^2-3^2=16\)

=>AH=4(cm)

AD=2*AH

=>AD=2*4=8(cm)

c: 

Xét tứ giác AHCF có

E là trung điểm chung của AC và HF

nên AHCF là hình bình hành

Hình bình hành AHCF có \(\widehat{AHC}=90^0\)

nên AHCF là hình chữ nhật

=>AH\(\perp\)AF và HC\(\perp\)FC

d: ABDC là hình thoi

=>\(\widehat{BAC}=\widehat{BDC}=60^0\)

ABDC là hình thoi

=>\(\widehat{ABD}+\widehat{BAC}=180^0\)

=>\(\widehat{ABD}=120^0\)

ABDC là hình thoi

=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

Bài 2:

a.

$P=M+N=-xy^2+3x^2y-x^2y^2+\frac{1}{2}x^2y-xy^2+\frac{-2}{3}x^2y^2$

$=(-xy^2-xy^2)+(3x^2y+\frac{1}{2}x^2y)+(-x^2y^2+\frac{-2}{3}x^2y^2)$

$=-2xy^2+\frac{7}{2}x^2y-\frac{5}{3}x^2y^2$

b.

$Q=N-M=(\frac{1}{2}x^2y-xy^2+\frac{-2}{3}x^2y^2)-(-xy^2+3x^2y-x^2y^2)$

$=(\frac{1}{2}x^2y-3x^2y)-xy^2+xy^2+(\frac{-2}{3}x^2y^2+x^2y^2)$

$=\frac{-5}{2}x^2y+\frac{1}{3}x^2y^2$

c.

$Q=\frac{-5}{2}(-1)^2.\frac{1}{2}+\frac{1}{3}(-1)^2.(\frac{1}{2})^2=\frac{-7}{6}$

Bài 3:
a. 

$A(x)=\frac{1}{3}x^2-2x^3+2x-\frac{4}{3}x^2-x-1$

$=-2x^3-x^2+x-1$

$A(x)$ có hệ số cao nhất là $-2$ và hệ số tự do là $-1$

$B(x)=2x^3+x^2+1$

$B(x)$ có hệ số cao nhất là $2$ và hệ số tự do là $1$

b.

$B(x)=(2x^3+2x^2)-(x^2-1)=2x^2(x+1)-(x-1)(x+1)$

$=(x+1)(2x^2-x+1)$

$B(-1)=(-1+1)(2x^2-x+1)=0$ nên $-1$ là nghiệm của $B(x)$

c.

$C(x)=A(x)+B(x)=-2x^3-x^2+x-1+(2x^3+x^2+1)$

$=x$

d.

$C(x)=0\Leftrightarrow x=0$

Vậy $x=0$ là nghiệm của $C(x)$

a: Xét tứ giác OAMD có

OA//MD

OD//AM

Do đó: OAMD là hình bình hành

mà \(\widehat{AOD}=90^0\)

nên OAMD là hình chữ nhật

a)

\(\left(x+1\right)\left(x-3\right)\left(x^2-2x\right)=-2\)

<=> (x + 1).(x - 3).x.(x - 2) = -2

<=> [ (x + 1). (x - 3) ]. [ x. (x - 2) ] = -2

\(\Leftrightarrow\left(x^2-2x-3\right).\left(x^2-2x\right)+2=0\) (1)

Đặt \(x^2-2x=a\)

PT (1) <=> (a - 3).a + 2 = 0

\(\Leftrightarrow a^2-3a+2=0\)

\(\Leftrightarrow a^2-a-2a+2=0\)

<=> a. (a - 1) - 2. (a - 1) = 0

<=> (a - 1). (a - 2) = 0

<=> a - 1 = 0 hoặc a - 2 = 0

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-1=0\\x^2-2x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)^2-2=0\\\left(x-1\right)^2-3=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1-\sqrt{2}\right).\left(x-1+\sqrt{2}\right)=0\\\left(x-1-\sqrt{3}\right).\left(x-1+\sqrt{3}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{2}\\x=1-\sqrt{2}\\x=1+\sqrt{3}\\x=1-\sqrt{3}\end{matrix}\right.\)

b) \(\left\{{}\begin{matrix}x^2+x-y^2-y=0\left(1\right)\\x^2+y^2-2\left(x+y\right)=0\left(2\right)\end{matrix}\right.\)

PT (1)\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+\left(x-y\right)=0\)

\(\Leftrightarrow\left(x-y\right)\left(x+y+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x+y=-1\end{matrix}\right.\)

TH1: x=y thay vào Pt (2) ta được: \(2x^2-4x=0\Leftrightarrow\left[{}\begin{matrix}x=0\Rightarrow y=0\\x=2\Rightarrow y=2\end{matrix}\right.\)

TH2: Thay x+y=-1 vào Pt (2) ta được: \(x^2+y^2+2=0\left(vn\right)\)

Vậy hẹ pt có nghiệm (x;y)=(0;0) ; (2;2)

hình 2 

a//b vì hai đường thẳng này cùng vuông góc với đường thẳng c

Gọi số CLB tối đa là x (nguyên dương).

Theo nguyên lý Dirichlet, từ 10 học sinh nào đó luôn có ít nhất \(\left[\dfrac{10+x-1}{x}\right]\) học sinh tham gia cùng 1 CLB

\(\Rightarrow\left[\dfrac{9+x}{x}\right]=3\Rightarrow\left[\dfrac{9}{x}+1\right]=3\)

\(\Rightarrow\left[\dfrac{9}{x}\right]+1=3\Rightarrow\left[\dfrac{9}{x}\right]=2\)

\(\Rightarrow2\le\dfrac{9}{x}< 3\Rightarrow3< x\le\dfrac{9}{2}\)

\(\Rightarrow x=4\)

Khi đó theo nguyên lý Dirichlet luôn tồn tại 1 CLB có ít nhất \(\left[\dfrac{35+4-1}{4}\right]=9\) học sinh