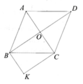
cho ngũ giác đều ABCDE.hai đường chéo AC và BE cắt nhau tại điểm K
Chứng minh ; a) Tứ giác ACDE là hình thang cân
b) Tứ giác CDEK là hình thoi
cần câu b) ạ !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số đo mỗi góc của ngũ giác đều là 1080.
Ta có tam giác ABC cân tại B
⇒ A 1 ^ = C 1 ^ = ( 180 0 − 108 0 ) : 2 = 36 0 ⇒ E A C ^ = D C A ^ (1)
Chứng minh tương tự ta được:
C 3 ^ = E ^ 1 = 36 0 ⇒ C 2 ^ = 36 0
Có C 2 ^ = E 1 ^ = 36 0 ⇒ E D / / A C (2)
Từ (1) và (2), suy ra ACDE là hình thang cân (ĐPCM)
(Các khác: Có thể chứng minh hình thang ACDE có hai đường chéo bằng nhau)
* Chứng minh tương tự ta có J E F ^ = E F G ^ = F G H ^ = G H I ^ = H I J ^ = I J E ^ .
Vậy tứ giác CDEK là hình bình hành
mà CD = DE, suy ra hình bình hành CDEK là hình thoi (ĐPCM)

Giải:
Góc của ngũ giác đều là \(\frac{\left(5-2\right).180^0}{5}=108^0\)
Xét \(\Delta ABC\)cân tại B có \(\widehat{ABC}=108^0\Rightarrow\widehat{A_1}=\widehat{C_1}=\frac{180^0-108^0}{2}=36^0\)
Do đó: \(\widehat{A_2}=\widehat{C_2}=108^0-36^0=72^0\)
Ta có: \(\widehat{C_2}+\widehat{D}=72^0+108^0=180^0\)mà 2 góc này ở vị trí trong cùng phía nên AC // DE.
Chứng minh tương tự như trên, BE // CD. Do đó CKED là hình bình hành.
Mà CD=DE nên CKED là hình thoi.
Mình làm mệt quá, k mk nha!

a: Xét ΔAEB và ΔCFD có
AE=CF
\(\widehat{EAB}=\widehat{FCD}\)
AB=CD
Do đó: ΔAEB=ΔCFD
Suy ra:BE=FD
Xét ΔADE và ΔCBF có
AE=CF
\(\widehat{DAE}=\widehat{BCF}\)
AE=CF
Do đó: ΔADE=ΔCBF
Suy ra: DE=BF
Xét tứ giác BEDF có
BE=DF
DE=BF
Do đó: BEDF là hình bình hành

cj kham khảo
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 1800
Tổng các góc trong của ngũ giác ABCDE là 1800. 3 = 5400
b) Vì ABCDE là ngũ giác đều nên
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)
Mặt khác ΔABC cân tại B nên
\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)
\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)
\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt)
nên tứ giác CEFD là hình thoi.

THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông

a) Ta thấy: Tứ giác BKQC nội tiếp đường tròn => ^CKQ = ^CBQ (2 góc nội tiếp cùng chắn cung CQ) (1)
Ta có: MK // AD => ^CKM = ^CAD (Đồng vị) . Mà ^CAD = ^CBD (Cùng chắn cung CD) => ^CKM = ^CBD (2)
Từ (1) và (2) => ^CKQ = ^CKM => 2 tia KQ và KM trùng nhau => 3 điểm K,M,Q thẳng hàng (đpcm).
b) Sửa đề: "5 điểm M,S,Q,R,T thẳng hàng ?"
Chứng minh tương tự câu a, ta có: 3 điểm L,M,R thẳng hàng => ^RMQ = ^KML (Đối đỉnh)
Tứ giác AKML là hình bình hành => ^KML = ^KAL = ^CAD. Do đó; ^RMQ = ^CAD (3)
Lại có: ^RTQ = ^RED (Cùng chắn cung RD); ^RED = ^CED = ^CAD => ^RTQ = ^CAD (4)
Từ (3) và (4) => ^RMQ = ^RTQ => Tứ giác RTMQ nội tiếp hay 4 điểm R,T,M,Q thuộc 1 đường tròn (*)
Mặt khác: ^TRS = ^BDE = ^BCE = ^TQS => Tứ giác TRQS nội tiếp hay 4 điểm T,R,Q,S thuộc 1 đường tròn (**)
Từ (*) và (**) => 5 điểm M,S,Q,R,T cùng thuộc 1 đường tròn (đpcm).
c) Giả sử S là 1 điểm chung của (PQR) và (O). Kẻ tia tiếp tuyến Fx của (O). Ta chứng minh Fx cũng là tiếp tuyến của (PQR)
Thật vậy: Gọi giao điểm thứ hai của AF với (PQR) là N. Kéo dài tia AP cắt (O) tại I.
Do L,M,R thẳng hàng; ML // AC => MR // AC => ^RMF = ^CAF (Đồng vị). Mà ^CAF = ^REF
Nên ^RMF = ^REF => Tứ giác EMRF nội tiếp => ^RFM = ^REM hay ^RFN = ^REM
Ta thấy: ^RFN = ^RPN => ^REM = ^RPN. Do 2 góc này đồng vị nên PN // EM hoặc PN // BE (5)
Xét đường tròn (O): 2 dây CD // BE => (BC=(DE => ^BAC = ^EAD
Có ^MAB = ^PAE => ^MAB - ^BAC = ^PAE - ^EAD => ^CAF = ^DAI => (CF=(ID
Xét (O): (CF = (ID, F và I nằm cùng phía so với CD => IF // CD => IF // BE (6)
Từ (5) và (6) => PN // IF => ^FIA = ^NPA (Đồng vị)
Dễ dàng c/m được PF = PI (\(\Delta\)PCF = \(\Delta\)PDI) => ^PIF = ^PFI hay ^FIA = ^PFI
Ta lại có: ^PFx = ^PFI + ^IFx = ^FIA + ^FAI = ^NPA + ^FAI = ^NPA + ^NAP = ^FNP (Góc ngoài)
Mà ^FNP = 1/2.Sđ(FP => ^PFx = 1/2.Sđ(FP => Fx là tia tiếp tuyến của đường tròn (PQR) => Đpcm.
Sorry, "5 điểm M,S,Q,R,T cùng nằm trên 1 đường tròn", mik gõ lộn :(
a: góc BAE=góc BCD=góc ABC=góc AED=góc CDE=108 độ
góc BAC=góc BCA=(180-108)/2=36 độ
=>góc CAE=góc ACD=72 độ
Vì góc CAE+góc AED=180 độ
nên AC//ED
mà góc AED=góc CDE
nên ACDE là hình thang cân
b: góc ABE=góc AEB=(180-108)/2=36 độ
góc AKE=180 độ-72 độ-36 độ=72 độ=góc ACD
=>KE//DC
Xet tứ giác KCDE có
KC//DE
KE//CD
KC=CD
DO đó: KCDE là hình thoi