cho tam giác ABC vuông tại A, AB= 5cm, AC=12 cm. I là trung điểm của AC. D chạy trên BC, E đối xứng với D qua I.
a) cm ADCE là hình gì vì sao
b) D phải ở vị trí nào trên BC thì ADCE là hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 11 2019
a) Xét tứ giác ADCE có:
I là trung điểm AC (gt), I là trung điểm DE(gt),. AC giao DE tại I (h.vẽ)
\(\Rightarrow ADCE\)là hbh
b) Để\(ADCE\)là hình thoi
\(\Leftrightarrow AD=DC\)
\(\Rightarrow\Delta ADC\)là tam giác cân tại D
\(\Rightarrow\widehat{A1}=\widehat{C1}\left(1\right)\)
Ta có: \(\widehat{A1}+\widehat{A2}=\widehat{A}=90^0\left(2\right)\)
Vì tam giác ABC vuông ở A nên \(\widehat{B}+\widehat{C1}=90^0\)( 2 góc phụ nhau ) (3)
Từ (1) và (3) \(\Rightarrow\widehat{B}+\widehat{A1}=90^0\)(4)
Từ (2) và (4) \(\Rightarrow\widehat{B}=\widehat{A2}\)
\(\Rightarrow\Delta ABD\)cân ở D
\(\Rightarrow BD=AD\)mà AD=DC
\(\Rightarrow AD=\frac{1}{2}BC\)
Xét tam giác ABC vuông ở A có: \(AD=\frac{1}{2}BC\)
\(\Rightarrow AD\)là đường trung tuyến của tam giác ABC
\(\Rightarrow D\)là trung điểm của BC.
Vậy D phải ở vị trí là trung điểm của BC thì \(ADCE\)là hình thoi.
+) Áp dụng định lý Py-ta-go vào tam giác ABC vuông ở A ta được:
\(AB^2+AC^2=BC^2\)
\(5^2+12^2=BC^2\)
\(169=BC^2\)
\(\Rightarrow BC=13\)mà \(DC=\frac{1}{2}BC\)( D là TĐ BC)
\(\Rightarrow DC=\frac{1}{2}.13=6,5\)
Vậy khi đó cạnh hình thoi ADCE là =6,5cm
13 tháng 11 2019
a) Xét tứ giác ADCE có: IA = IC (gt)
ID = IE (gt)
=> tứ giác ADCE là hình bình hành
b) Để hình bình hành ADCE là hình thoi
<=> AD = DC
<=> t/giác DAC cân tại D
<=> \(\widehat{DAC}=\widehat{DCA}\)
Do \(\widehat{B}+\widehat{BCA}=90^0\)
\(\widehat{BAD}+\widehat{DAC}=90^0\)
=> \(\widehat{B}=\widehat{BAD}\) <=> t/giác ABD cân tại D
<=> BD = AD (cùng = AD)
<=> D là trung điểm của BC
Áp dụng định lí Pi - ta - go vào t/giác ABC vuông tại A
Ta có: BC2 = AB2 + AC2
=> BC2 = 52 + 122 = 25 + 144 = 169
=> BC = 13 (cm)
Do D là trung điểm của BC
=> BD = DC = 1/2BC = 1/2.13 = 6,5(cm)
Vậy ...
4 tháng 12 2021
a: Xét tứ giác ADCE có
I là trung điểm của AC
I là trung điểm của DE
Do đó: ADCE là hình bình hành
mà AD=CD
nên ADCE là hình thoi
CM
3 tháng 6 2017
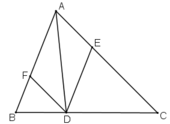
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).